どうも、木村(@kimu3_slime)です。
今回は、ソボレフ空間\(W^{k,p},H^k\)とは何か、多重指数、ノルム、内積について、弱微分を前提知識として紹介します。
ソボレフ空間と多重指数
\(\Omega\subset \mathbb{R}^N\)、\(k\)を非負の整数、\(1 \leq p \leq \infty\)としましょう。
ソボレフ空間\(W^{k,p}\)は、\(p\)乗可積分\(u \in L^{p}\)、かつ\(k\)階までの弱微分\(D^{\alpha} u\)が存在し、それらがすべて\(p\)乗可積分\(D^{\alpha} u\in L^{p} \)となる関数のなす線形空間です。
\[W^{k,p}(\Omega):=\{u \mid すべての多重指数\alpha に対し、\\0 \leq |\alpha| \leq k ならば D^{\alpha} u \in L^p(\Omega)\}\]
特に\(p=2\)のケースをよく使うため、
\[H^k(\Omega) := W^{k,2}(\Omega)\]
という記号があります。
登場した多重指数\(\alpha\)は、多変数の弱微分を統一的に表すための記法です。
例えば、2変数の2回(弱)偏微分には
\[\frac{\partial ^2 u}{\partial x^2 },\frac{\partial ^2 u}{\partial x \partial y },\frac{\partial ^2 u}{\partial y^2 }\]
などの可能性があります。こうした偏微分を書き下すのは、変数や微分の回数が増えるほど困難です。
そこで各変数における微分の回数を表す、多重指数(multi-index)というものを使って、これらの微分を表しましょう。たとえば、
\[D^{(2,0)}u:=\frac{\partial ^2 u}{\partial x^2 }\]
\[D^{(1,1)}u:=\frac{\partial ^2 u}{\partial x \partial y }\]
\[D^{(0,2)}u:=\frac{\partial ^2 u}{\partial y^2} \]
です。2変数の場合、\(\alpha = (\alpha_1,\alpha_2)\)で、\(\alpha_1,\alpha_2\)を非負の整数とします。
\(D^{\alpha}u\)を、第1変数\(x\)について\(\alpha_1\)回偏微分、第2変数\(y\)について\(\alpha_2\)回偏微分した関数を表すものとします。
そして、各指数の和を\(|\alpha|:= \alpha_1+\alpha_2\)と書き、多重指数の次数(order)や長さと呼びます。
こうすれば、2階偏微分の\(L^p\)ノルムの和は
\[\sum_{|\alpha|=2 }\|D^\alpha u\|_{L^p}^p\]
といったように表せるわけです。
\(N\)変数ならば、多重指数\(\alpha=(\alpha_1,\dots,\alpha_N)\)とは、\(N\)個の非負整数\(\alpha_1,\dots,\alpha_N\)の組(順序対)です。次数は\(|\alpha|:=\alpha_1+\cdots+\alpha_N\)です。
そして多重指数を使った微分の記法として、
\[D^{\alpha}u:= \frac{\partial^{|\alpha|} u }{\partial x_1 ^{\alpha_1} \cdots \partial x_N ^{\alpha_N}}\]
と表すことにします。
\(|\alpha|=0\)、すなわち\(\alpha =(0,\dots,0)\)のときは、\(\alpha\)回の微分とは何もしないこと、\(D^{\alpha} u =u\)とします。
ソボレフ空間のノルム、内積
多重指数の記法と\(L^p\)ノルムを用いると、ソボレフ空間\(W^{k,p}\)に次のノルムを定義できます。
\[\|u\|_{W^{k,p}}:=(\sum_{0 \leq |\alpha| \leq k} \|D^{\alpha}u\|_{L^p}^p)^\frac{1}{p}\]
すなわち、\(k\)階までのすべての偏導関数\(D^{\alpha}u\)の\(L^p\)ノルムの\(p\)乗を足し合わせ、全体を\(\frac{1}{p}\)乗したものです。
特に\(k=0\)のときは、\(|\alpha|=0\)となる多重指数は\(D^{\alpha}u =u\)しかないので、
\[\|u\|_{W^{0,p}}= (\|u\|_{L^p}^p)^\frac{1}{p}=\|u\|_{L^p}\]
となります。すなわち、\(W^{k,p}\)のノルムは、\(L^p\)ノルムの一般化です。
\(\|u\|_{W^{k,p}}\)はノルムの定義を満たし、ソボレフ空間\(W^{k,p}\)はノルム空間となります(\(L^p\)ノルムの性質を用いて示せます)。さらに、\(W^{k,p}\)は完備なノルム空間、すなわちバナッハ空間となることが知られています。
\(p=2\)のケースでは、ノルムだけでなく内積も定義できます。\(H^k=W^{k,2}\)の関数\(u,v\)に対し、
\[\langle u,v\rangle_{H^k}:=\sum_{0 \leq |\alpha| \leq k} \langle D^\alpha u, D^{\alpha} v\rangle_{L^2}\]
と定めると、これは内積の定義を満たし、\(H^k\)は内積空間となります(\(L^2\)内積の性質を用いて示せます)。\(H^k\)は完備な内積空間、すなわちヒルベルト空間となることが知られています。
具体例
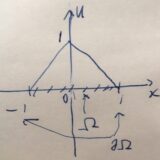
最後に、\(W^{1,2}((-1,1))\)において、\(u(x)=|x|\)のノルムを具体的に計算してみましょう。
ノルムを求めるためには、各微分を求め、その積分ノルムを計算し、足し合わせる必要があります。
弱微分は
\[ u^{\prime}(x)= \left\{ \begin{array}{lr} -1 && (-1<x\leq 0) \\ 1 && (0<x< 1) \end{array} \right. \]
となります。したがって、
\[\begin{aligned} &\|u\|^2_{L^2} \\&= \int_{-1}^1 |x|^2 dx\\ &= \int_{-1}^1 x^2 dx \\ &=[\frac{1}{3}x^3]_{-1}^1 \\&=\frac{2}{3} \end{aligned}\]
\[\begin{aligned} &\|u^{\prime}\|^2_{L^2} \\&= \int_{-1}^1 |u^{\prime}(x)|^2 dx\\ &= \int_{-1}^1 1 dx \\ &=2 \end{aligned}\]
となるので、
\[\begin{aligned} &\|u\|_{W^{1,2}} \\ &=(\|u\|_{L^2}^2 +\|u^{\prime}\|_{L^2}^2)^{\frac{1}{2}} \\ &=(\frac{8}{3})^{\frac{1}{2}}\end{aligned}\]
と求めることができました。
以上、ソボレフ空間\(W^{k,p},H^k\)とは何か、多重指数、ノルム、内積を紹介してきました。
ソボレフ空間は完備性を持つので、一般的な偏微分方程式における微分を弱微分として捉えた方程式における解(弱解)の構成に役立てることができます。
その議論では、多重指数を使った微分\(D^\alpha u\)やノルム\(\|u\|_{W^{k,p}}\)を用いるわけですが、今回の話で定義や簡単な例を知ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
連続関数、可積分関数の線形空間(関数空間)、微分と積分の線形性とは