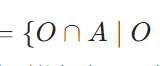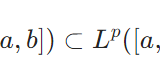ほとんど至る所（a.e.）とは：簡単な関数を例に

どうも、木村（@kimu3_slime）です。

今回は、ほとんど至る所（a.e.）とは：簡単な関数を例に、ルベーグ積分の前提知識をできるだけ少なめに紹介します。

用例
定義
ディリクレ関数
こちらもおすすめ

用例

数学において、「ごく一部分を除いて良い性質を持つ」状況が起こります。

例えば、\(f(x)=\frac{1}{x}\)は、\(x \neq 0\)を除いて\(\mathbb{R}\)上連続です。このことを、「\(f(x)=\frac{1}{x}\)は、\(\mathbb{R}\)上ほとんど至る所で連続」と言います。

また、\(g(x)=|x|\)は、\(x \neq 0\)を除いて\(\mathbb{R}\)上で微分可能です。このことを、「\(g(x)=|x|\)は、\(\mathbb{R}\)上ほとんど至る所で微分可能」と言います。

定義

「全体集合\(X\)のほとんど至る所で性質\(P(x)\)が成り立つ」とは、\(P(x)\)が成り立たない例外があってもよく、そのような例外はごく一部分であることを意味しています。

さきほどの例では、全体集合は\(X=\mathbb{R}\)で、\(N=\{0\}\)という一点集合が例外でした。「\(X\)から\(N\)を除いた集合、差集合\(X \setminus N\)においては関数が連続、微分可能」といった状態を「ほとんど至る所」という言葉で表現したわけです。

例外が無視して良いかどうかを決める基準は、測度（measure）という概念にあります。測度は長さや面積、体積といった測ることを抽象化した集合を変数とする関数で、ルベーグ積分論の基礎概念です。

日常的な意味で使われる長さに対応する測度、1次元のルベーグ測度\(\mu\)は、開区間\((a,b)\)や閉区間\([a,b]\)に対し、

\[\mu ((a,b)) = b-a\]

\[\mu ([a,b]) = b-a\]

という性質を満たします。例えば、\(\mu ([0,1])=1\)で、まさに区間の長さを表すものと言えます。

このルベーグ測度という基準において、一点集合\(\{0\}\)を測るとどうなるでしょうか。それは幅を持たず、長さが0と予想できます。実際、\(\mu ([0,\frac{1}{n}]) = \frac{1}{n} \to 0\,(n \to \infty)\)で、\(\mu(\{0\})=0\)です（点には大きさがない）。（測度はある種の連続性：単調列連続性を持ちます）

そして、一点集合のように測度が0になる集合を「無視できるもの」として扱います。正式には、\(\mu(N)=0\)を満たす（可測）集合\(N\)を、ゼロ集合（null set）と呼びます。

全体集合\(X\)のおいて定義されている命題\(P(x)\)について考えましょう。\(P(x)\)が\(X\)においてほとんど至る所（almost everywhere）成り立つとは、\(A:=\{x \in X \mid P(x)が成り立たない\}\)がゼロ集合となることです。

例えば、「\(f(x)=\frac{1}{x}\)は、\(\mathbb{R}\)上ほとんど至る所で連続です。なぜなら、連続でない点の集合は\(A=\{0\}\)で、\(A\)はゼロ集合（\(\mu(A)=0\)）だからです。

\[ v(x)= \left\{ \begin{array}{lr} -1 && (-1<x\leq 0) \\ 1 && (0<x< 1) \end{array} \right. \]

\[ w(x)= \left\{ \begin{array}{lr} -1 && (-1<x< 0) \\ 1 && (0\leq x< 1) \end{array} \right. \]

と置くと、\((0,1)\)上ほとんど至る所で\(v(x)=w(x)\)です。

\(v(0)=-1\)、\(w(0)=1\)で、\(v(x)\neq w(x)\)となるのは\(x=0\)のみです。したがって、\(A=\{x \in (0,1) \mid v(x) \neq w(x)\}=\{0\}\)となり、\(\mu(A)=0\)なので、ほとんど至る所で関数は一致します。

ほとんど至る所で関数が等しいことを、\(v=w \,\mathrm{a.e.}\)と書くこともあります。a.e.はalmost everywhereを省略したものですね。

一致しない例として、

\[ u(x)= \left\{ \begin{array}{lr} -1 && (-1<x\leq 0) \\ 0&& (0< x< 0.001) \\1 && (0.001\leq x< 1) \end{array} \right. \]

を考えましょう。「\((-1,1)\)上で\(u =v \, \mathrm{a.e.}\)」ではありません。

なぜなら、等しくない部分の集合は\(\{x \in (0,1)= u(x) \neq v(x)\} =(0,0.001)\)で、\(\mu((0,0.001))=0.001 \neq 0\)、ゼロ集合ではないからです。\((0,0.001)\)はごく小さな部分ではありますが、正の長さを持っており、無視できません。

ディリクレ関数

ゼロ集合の例として、ここまでは一点集合を挙げてきました。

2点や3点、有限個の点の集合は（ルベーグ測度において）ゼロ集合です。定義域が有限個の区間に分かれていて、その区間の端点を除いて連続な関数、区分的に連続な関数は、定義域のほとんど至る所で連続と言えます。

（ちなみに、1点集合が測度0になるのは、今回考えているのがルベーグ測度だからです。一般には、一点集合が測度0とは限りません。例として数え上げ測度があります。）

ルベーグ積分論に慣れていない人は奇妙に思うかもしれませんが、要素の個数が無限個であっても、測度0になることはありえます。

\(\mathbb{R}\)においてルベーグ測度を考えると、有理数全体の集合\(\mathbb{Q}\)は測度0です \(\mu(\mathbb{Q})=0\)。測度には可算加法性という性質があり、可算無限個の集合までなら、分割して計算できます。\(\mathbb{Q}\)は可算無限集合なので、一点集合の測度の可算無限個の和、0の無限和として0になるわけです。

この性質を活かした関数

\[ f(x)= \left\{ \begin{array}{lr} 1 && (x\in \mathbb{Q}) \\ 0 && (x \in \mathbb{R}\setminus \mathbb{Q}) \end{array} \right. \]

について考えましょう。これは有名な例で、ディリクレ関数（Dirichlet function）と呼ばれています。

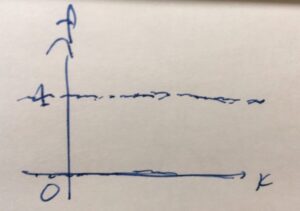
有理数となる点では1、無理数となる点では0という値を取る関数です。例えば、\(f(\frac{22}{7})=1\)、\(f(\pi)=0\)です。

実数全体において有理数の集合は稠密で、どんなに小さな区間に注目しても、有理数と無理数が含まれているため、グラフは上の図のように、0,1を示す直線に見えます。ただし、そう見えるだけで、個別に点\(x\)を決めれば、\(f(x)\)は0,1のいずれかですが。

ディリクレ関数は、恒等的に0の関数と\(\mathbb{R}\)上でほとんど至る所等しいです \(f=0 \,\mathrm{a.e.}\)。なぜなら、一致しない点の集合は\(A=\{x\in \mathbb{R} \mid f(x) \neq 0\}=\mathbb{Q}\)で、\(\mu(\mathbb{Q})=0\)だからです。

有理数は可算無限集合で、無理数や実数全体は非可算無限集合です。有理数の集合は、無限集合ではありますが、（ルベーグ）測度という観点から見ると、はるかにスカスカで、大きさを持たない集合とみなしているわけです。

手書きのグラフからは読み取れませんが、ディリクレ関数は「飛び飛びの点」で1を取っていて、べったりと連続的には0の値を取っている関数と言えます。ほとんど至る所では、恒等的に0の関数と一致するわけです。

（ちなみに、非可算無限集合だからといって、測度0でないとは限りません。例：カントール集合）

以上、ほとんど至る所（a.e.）とは：簡単な関数を例に紹介してきました。

ルベーグ積分論やその応用分野では、「ほとんど至る所」という用語を用いることによって、細かな違いを無視さえすれば都合の良い性質を持つことを表現できます。たとえば不連続点を除いたフーリエ級数の収束や、弱微分のほとんど至る所で一致する関数としての一意性です。

今回の例でイメージはつかめたとは思いますが、より詳しく学びたい人は、ルベーグ積分論や測度論を学んでみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。