どうも、木村(@kimu3_slime)です。
今回は、方程式をyについて解く・文字について解く方法を紹介します。
yについて解く方法と意味
\[x+2y=6\]
を\(y\)について解きましょう。
この問題は平成20年度全国学力・学習状況調査、中学校数学Aの問題2(4)で、正答率は55.0%となっています。
方程式を\(y\)について解くとは、\(y\)を他の数字や文字を使って表すこと、\(y= ???\)という形に式を変形することです。やってみましょう。
まず、両辺に\(-x\)を加えると(\(x\)を引くと)、
\[x+(-x)+2y=6+(-x)\]
\[2y=6-x\]
となります。\(2y\)を\(y\)にしたいので、両辺に\(\frac{1}{2}\)をかけると(2で割ると)
\[\frac{1}{2}\times 2y =\frac{1}{2}(6-x)\]
\[y =\frac{1}{2}(6-x) \]
となりました。これが\(y\)について解くということです。
ちなみに、\(x,y\)という2つの文字を持つ等式を\(y\)について解くことは、それを関数\(y =\frac{1}{2}(6-x) \)として表しやすくしてくれます。
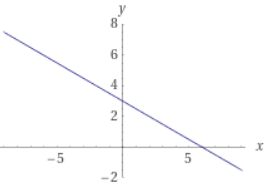
画像引用:WolframAlpha
ありがちな間違いとして気をつけたいのが、両辺に\(\frac{1}{2}\)をかける(2で割る)ときに、
\[2y=6-x\]
\[\frac{1}{2}\times 2y =\frac{1}{2}\times 6-x\]
\[y= 3-x\]
としてしまうことです。\(\frac{1}{2}\)が右辺全体でなく、第1項にしかかかっていません。これでは結果がずれてしまいます。
\[x+2y=6\]
を\(y\)について解けると、何が嬉しいのでしょうか。
例えば\(x=1,2,3\)のときの等式を書いてみると、
\[1+2y=6\]
\[2+2y=6\]
\[3+2y=6\]
という3つの等式ができます。
\(y\)について解けた等式\(y =\frac{1}{2}(6-x) \)を用いれば、これらの解はそれぞれ、\(x=1,2,3\)を代入した、\(y=\frac{5}{2},2,\frac{3}{2}\)と求めることができます。個別に問題を解かなくても、一気に解けるわけです。
文字(未知数)を含む等式が解けることは、その文字がどんな数値であっても解が求められる、一般的に解けると言えますね。
xについて解く方法
さて、同じ等式
\[x+2y=6\]
を\(x\)について解いてみましょう。
注目する文字について解くとは、「その文字=何か他の数字や文字」という形で表すことです。
今回は\(x\)について解くので、左辺から\(2y\)を消すために、両辺に\(-2y\)を加えると、
\[x+2y-2y=6-2y\]
\[x=6-2y\]
と\(x\)について解くことができました。
次の方程式を解きましょう。
\[x+2=6\]
という問題はよくあるものです。この等式は1種類の文字\(x\)しか含んでいないので、「(\(x\)について)解く」という前提が省略された書き方になっています。
一方で、「\(x+2y=6\)という方程式を解きなさい」という文は、問題として成立していません。2つの文字\(x,y\)を含んでいて、\(x\)について解くのか、\(y\)について解くのか、注目する文字(変数)がはっきりとしないからですね。
3つ以上の文字を含むとき
3つ以上の文字を含むときも、ある文字について解く問題は考えられます。
三角形の面積\(S\)は、底辺の長さを\(a\)、高さを\(h\)とするとき、
\[S= \frac{1}{2}ah\]
と表せます。これを\(a\)について解きましょう。
この問題は平成21年度全国学力・学習状況調査、中学校数学Aの問題2(4)で、正答率は45.7%となっています。
\(a\)について解くために、まず左辺と右辺を入れ替えましょう。\(a\)が右辺にあっても問題はないのですが、慣習的に左辺に1文字だけの形に表すことが多いです。
\[ \frac{1}{2}ah=S\]
両辺に2をかければ、
\[ 2 \times \frac{1}{2}ah=2 S\]
\[ah=2 S\]
さらに両辺を\(h\)で割れば、
\[a = \frac{2S}{h}\]
と\(a\)について解くことができました。
この解は、次のように利用できます。面積が\(4\)、高さが\(2\)の三角形があるとき、底辺の長さはいくつでしょうか。代入すれば、\(a=\frac{2\cdot 4}{2}=5\)と求められますね。
以上、方程式をyについて解く・文字について解く方法を紹介してきました。
文字を使うと、さまざまな問題を一般的にまとめて扱うことができます。複数の文字の関係は複雑になりがちですが、ひとつの文字に注目して解くことができれば、関係性が見えやすくなるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)
こちらもおすすめ
ルートを含む等式の両辺を2乗するときの注意点:逆も成り立つか