どうも、木村(@kimu3_slime)です。
今回は、平行でない直線の同位角・錯角とは:問題から考えていきましょう。
平行でない直線の同位角
まずは同位角に関する問題です。
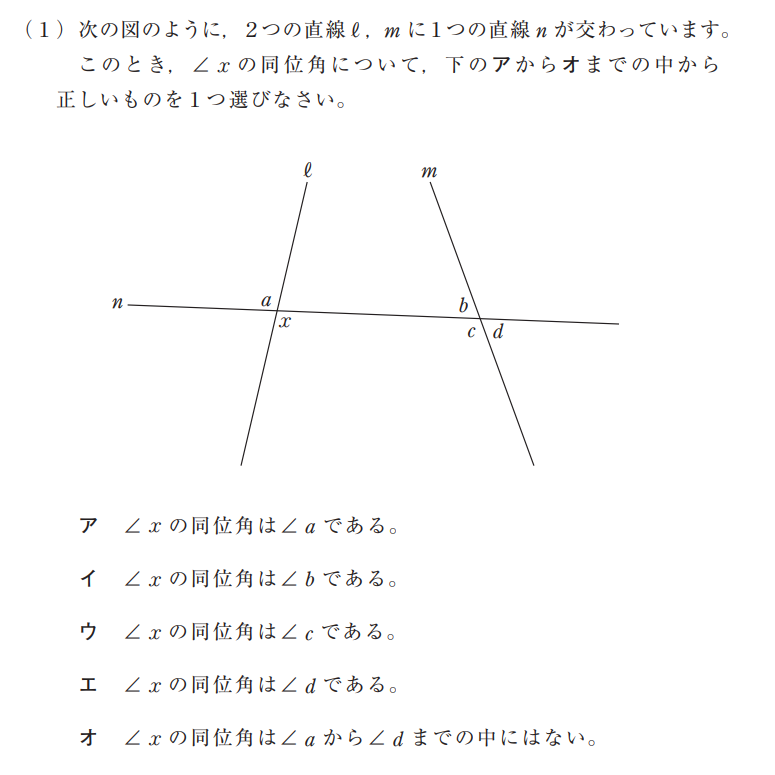
画像引用:平成21年度中学校数学A
これは平成21年度全国学力・学習状況調査の中学校、数学Aの問題6(1)です。正答率は42.0%。
では、考えていきましょう。
直線\(\ell,m\)があり、それを直線\(n\)が横断しています。それらが交わってできる角の関係性に関する問題です。
交わった点から右下側にある角として、\(\angle x, \angle d\)がありますね。
おそらく、迷うのは次の2つの選択でしょう。
- \(\angle x \)の同位角は\(\angle d\)である。
- \(\angle x \)の同位角は\(\angle a\)から\(\angle d\)までの中にはない。
直線\(\ell,m\)は、文章としては書かれていませんが、おそらく平行ではないと思われます。
それでも、同じく交わった点に対して右下側の角は、同位角と呼んで良いのでしょうか?
たとえ2つの直線が平行でなくても、位置関係が同じ角は同位角と呼ぶことになっています(言葉の約束、定義)。したがって、\(\angle x \)の同位角は\(\angle d\)が答えですね。
「同位角の大きさは等しい」と呼ばれる性質がありますが、これは正確にいえば「平行線によってできる同位角の大きさが等しい」です。したがって、平行線によってできるわけではない同位角の大きさ、\(\angle x ,\angle d\)の角度は等しくなくても間違ってはいません。
ちなみに、「\(\angle x\)の同位角は\(\angle a\)である」という選択肢は、「\(\angle x\)の対頂角は\(\angle a\)である」とすれば正しくなります。
この問題で記号で示された角の中から、\(\angle x,\angle d\)以外に、同位角の組を探してみてください。
答えは、\(\angle a, \angle b\)ですね。共に左上側にあります。
平行でない直線の錯角
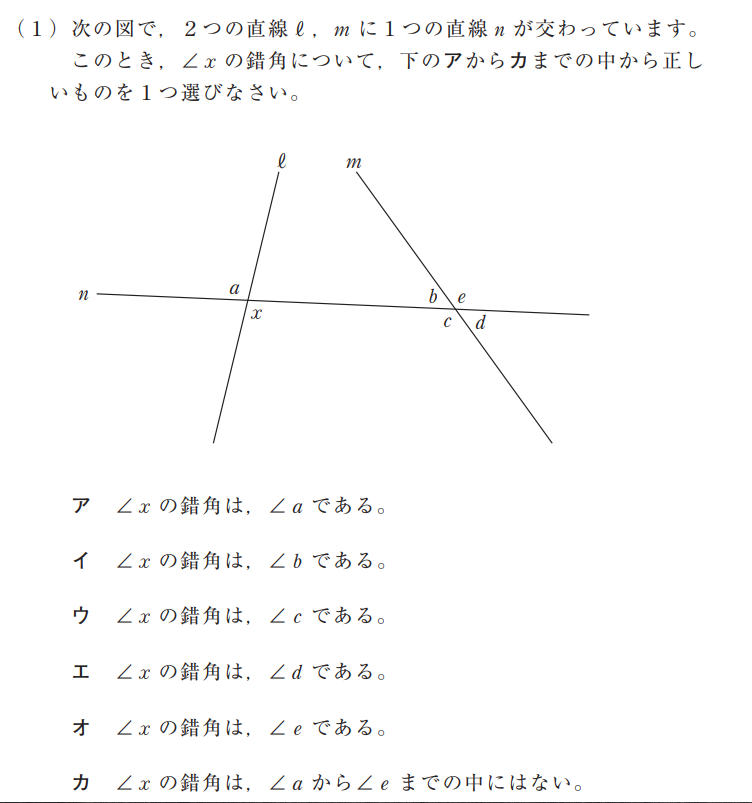
画像引用:平成29年度中学校数学A
これは平成29年度全国学力・学習状況調査の中学校、数学Aの問題6(1)です。正答率は42.6%。
では、考えていきましょう。
\(\ell,m\)の内側にあって、\(n\)をまたいで反対側にある角の候補として、\(\angle x, \angle b\)があります。
おそらく、迷うのは次の2つの選択でしょう。
- \(\angle x \)の錯角は\(\angle b\)である。
- \(\angle x \)の錯角は\(\angle a\)から\(\angle d\)までの中にはない。
同位角と同様に、錯角もまた、平行でない直線に対しても定義されます。したがって、「\(\angle x \)の錯角は\(\angle b\)である」が正解です。
「錯角の大きさは等しい」と呼ばれる性質がありますが、これは正確にいえば「平行線によってできる錯角の大きさが等しい」です。したがって、平行線によってできるわけではない錯角の大きさ、\(\angle x ,\angle b\)の角度は等しくなくても間違ってはいません。
この問題で記号で示された角の中から、\(\angle x,\angle b\)以外に、錯角の組を探してみてください。
答えは、\(\angle a, \angle d\)ですね。\(\ell, m\)の外側であり、横断線\(n\)に対して反対側にあります。
以上、平行でない直線の同位角・錯角とは:問題から考えてきました。
同位角や錯角という言葉を使うときは、平行線に関する場合が多いかもしれません。
しかし、2本の直線とそれを横断する直線さえあれば、位置関係から同位角や錯角が定義できるので、見抜けるようになりましょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)