どうも、木村(@kimu3_slime)です。
今回は、表から1次関数の変化の割合を求める問題の考え方を解説します。
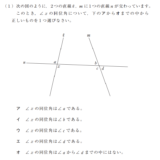
これは平成25年度全国学力・学習状況調査の中学校数学A問題11(2)です。正答率は43.3%となっています。
では、解説していきましょう。
この問題を解くためには、
- 1次関数とは何か
- 関数の変化の割合とは何か
の2つを知っておく必要があります。
1次関数とは、\(y=2x+3\)のように、\(x\)の1次多項式\(y=ax+b\)によって定まる関数です。そのグラフは直線形になるので、線形関数とも呼ばれます。
関数の変化の割合\(r\)とは、
\[r=\frac{yの変化量}{xの変化量}\]
によって表される数のことです。おおざっぱに言えば、\(x\)の値が1だけ増える間に、\(y\)の値はどれだけ増えますか、ということを表します。
変化量は、2つの数字を指定することによって決まります。\(x\)を0から1まで変化させるとき、\((xの変化量)= 1-0=0\)です。また、そのときの\((yの変化量)= (x=1のときのyの値)- (x=0 のときのyの値)\)となります。
\(x\)を変化させる範囲は0、1でなくても良いです。ただし、きちんと\(x\)の変化に対応した\(y\)の変化を計算するようにしましょう。
では、表を眺めていきましょう。
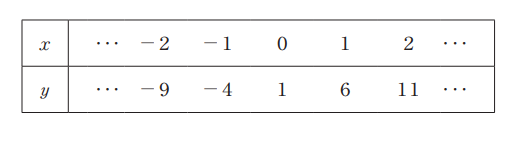
これは1次関数とあるので、まずこの情報をもとに、ラフで良いのでグラフを描いてみると良いでしょう。座標平面上に表にある2つの点を描き、その間を直線で結べばこの1次関数のグラフとなります。
たとえ指示されていなくても、的はずれな回答をしないためにイメージを持つのは大事です。
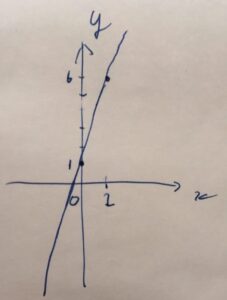
右肩上がりのグラフになりました。\(x\)が増えると\(y\)も増える関係になっていて、したがって変化率は正の数と予想できます。
特に、表の\(x=0,1\)の部分に注目しましょう。この2つの値において、\(x\)は\(1-0=1\)だけ変化しています。それにともなって、\(y\)は\(6-1=5\)だけ変化しています。よって、求める変化率は
\[ r = \frac{5}{1}=5\]
となりました。
つまり、表のごく一部分
| \(x\) | 0 | 1 |
| \(y\) | 1 | 6 |
の情報だけで、この問題に答えることはできます。
しかし、\(x=0,1\)以外に注目することでも、変化の割合を求めることはできます。やってみましょう。
\(x\)を-2から2まで変化させましょう。このとき、\(x\)の変化量は\(2-(-2)=4\)です。また、\(y\)の変化量は、表から\(11-(-9)=20\)です。よって、変化の割合は
\[ r = \frac{20}{4}=5\]
と求めることができました。

表の下側の\(y\)を見ると、\(-9,-4,1,6,11\)という数字の列を見ると、それが\(5\)ずつ増加しているという規則性にも気づきますね。これが変化の割合です。ただし、この方法で求められるのは、\(x\)が1ずつ変化するように表が書いてあるおかげであることに注意してください。
他の変化のさせかたでも、この変化の割合が求められることを確かめてみてください。
実は、どんな1次関数のどのような変化を考えても、変化の割合は一定です。そして変化の割合はグラフの傾きに一致します。
一般的に、1次関数\(y=ax+b\)の変化の割合を考えましょう。
\(x=0,1\)における\(x\)の変化は、\(1-0=1\)です。このとき、\(y\)は\((a\cdot 1+b)-(a\cdot 0+b)=a\)だけ変化します。よって、変化の割合は
\[r= \frac{a}{1}=a\]
と傾きに一致することが示せました。
つまり、1次関数とは、変化の割合が常に一定である関数と言えます。
これは1次関数の著しい性質で、一般的な関数は、変化の割合は考える変化の場所や幅の大きさによって変わります。
今回の問題では「変化の割合を求めましょう」と、これといって変化する区間が指定されていませんが、一般にはそれが指定されなければ変化の割合は定まりません。
「\(x\)が\(-2\)から\(2\)まで変化するときの、関数の変化の割合を求めましょう」といった指定が必要です。
以上、表から1次関数の変化の割合を求める問題の考え方を解説をしてきました。
「変化の割合は1次関数の傾きに一致」という性質を知っていれば、答えを求めるのは機械的にできます。しかし、そもそも変化の割合とは何かということを、図を書いて理解しておくとより良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)