文章題「yはxの関数である」の考え方を解説

どうも、木村（@kimu3_slime）です。

今回は、文章題「yはxの関数である」の考え方を解説します。

縦と横の長さの和が20cmの長方形について、「縦の長さを決めると、それにともなって面積がただ1つ決まる」という関係があります。

太字部分を

「　　」は「　　」の関数である

と表すとき、空白に当てはまる言葉を書きましょう。

これは平成29年度全国学力調査、中学生数学A、問題9です。正答率は21.1%となっています。

この問題に答えるためには、関数とは何かの知識が必要です。簡単に言えば、規則的な対応関係のことです。まずは具体的な例から考えていきましょう。

\(y=2x+1\)という等式を考えましょう。\(x=0\)のとき、\(y=1\)となります。\(x=1\)のとき、\(y=3\)ですね。このように、一方の変数\(x\)を決めると、それに対応する値\(y\)がただひとつ決まるとき、\(y\)は\(x\)の関数であると言います。関数\(f\)を\(f(x)=2x+1\)と表すこともあります。

単純な関数として知られているのは、\(y=2x+1\)のような1次関数です。この関数のグラフは直線的となり、線形関数とも呼ばれます。\(y=3x^2\)のような関数は、2次関数と呼ばれています。\(x\)と\(y\)の対応規則です。

たとえ\(2x+1\)や\(3x^2\)のように明示的な数式がわかっていなかったとしても、ある数\(x\)が決まるともう一つの数\(y\)がただひとつ決まるとき、それは関数と呼ばれます。

つまり、

「　　」は「　　」の関数である

の空白に入る言葉を求める問題は、

\(y\)は\(x\)の関数である

と書くとき、\(x,y\)に対応する数、量は何ですか、という問い掛けです。

何\(x\)が決まると、何\(y\)がただひとつ決まるのでしょうか。問題文には「縦の長さを決めると、それにともなって面積がただ1つ決まる」とあります。

まず先に決まるのが、（長方形の）縦の長さ\(x\)ですね。それに応じて、（長方形の）面積\(y\)がただひとつ決まるという関係に注目しています。よって、

「面積」は「縦の長さ」の関数である

が答えです。

今回の問題では、より具体的に関数を数式で表すことができます。やってみましょう。

長方形の縦の長さを\(x\)、横の長さを\(z\)とします。縦と横の長さの和が20cmなので、\(x+z=20\)で、\(z=20-x\)と表せます。

長方形の面積を\(y\)としましょう。それは縦×横で求められるので、\(y=xz=x(20-x)\)と表すことができました。これは2次関数です。

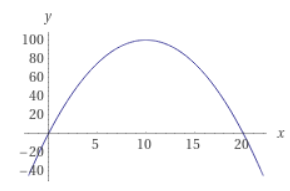
画像引用：WolframAlpha

例えば、縦の長さが\(x=10\)のとき、面積は\(y=10(20-10)=100\)です。この関数を分析すると、\(x=10\)のとき長方形の面積が最大になることが示せます。縦も横も10と等しいので、正方形になるときが一番大きくなるわけです。

\(x\)は辺の長さで、辺の長さの合計が20なので、\(0 \leq x \leq 20\)という範囲で変化するときの\(y\)の値に注目するでしょう。関数が定義される変数の範囲は、定義域と呼ばれます。

少し発展的な問題ですが、関数ではない例を挙げましょう。

「\(y\)は\(x\)の関数である」としても、「\(x\)が\(y\)の関数である」とは限らないのです。

「縦の長さ」は「面積」の関数である

とは言えないことを示しましょう。

関数の定義では、\(x\)に応じて\(y\)がただひとつに決まらなければならないことに注意しましょう。面積\(50\)の長方形の縦の長さは、ただひとつに決まるでしょうか？

決まりません。縦の長さ5、横の長さ10の長方形。縦の長さ10、横の長さ5の長方形。2つの可能性があります。面積50に対して、縦の長さは5または10です。ひとつの数に対して、2つの数が対応してしまっています。

つまり、\(x\)から\(y\)への対応：関数\(y=f(x)\)が決まったとしても、その逆の\(y\)から\(x\)への対応：逆関数\(x=f^{-1}(y)\)が決まるとは限りません。

参考：全単射と逆写像の存在が同値であることの証明、応用

最後にもう一つ、関数を見出す問題を扱いましょう。

画像引用：平成 26 年度　全国学力・学習状況調査中学校数学A、問題9

何を決めると、何がただひとつ決まるでしょうか。重量が決まると、料金がただひとつ決まりますね。これを「料金は重量の関数である」と言うわけです。

この関数は、1次関数や2次関数のように単純には表せませんが、場合分けして数式で表すことはできます。

\[ f(x)= \left\{ \begin{array}{lr} 150 && (0\leq x<100) \\ 190 && (100 \leq x< 250) \\ 270 &&(250\leq x <500) \\ 320 &&(500\leq x<1000)\end{array} \right. \]

この関数のグラフを描いてみてはいかがでしょうか。

以上、文章題「yはxの関数である」の考え方を解説してきました。

「時間が経つと太陽の（見かけの）位置が変わる」というように、一方が変化するとき、もう一方がどう変化するかという対応規則を調べるのは、科学の基本的な発想です。

現実における対応関係は1次関数や2次関数ほどシンプルではないかもしれません。しかし、単純化すればおよそ関数で説明できる現象は実に多いです。観測した2つのデータの対応関係を説明するために、関数や理論（数理モデル）を用いるのは数学の基本的な応用です。

その初歩的な発想として、何と何が対応しているのか見抜いて言葉にできるようになってみましょう。

木村すらいむ（@kimu3_slime）でした。ではでは。