どうも、木村(@kimu3_slime)です。
今回は、角錐・円錐の体積はなぜ1/3か:積分による証明を紹介します。
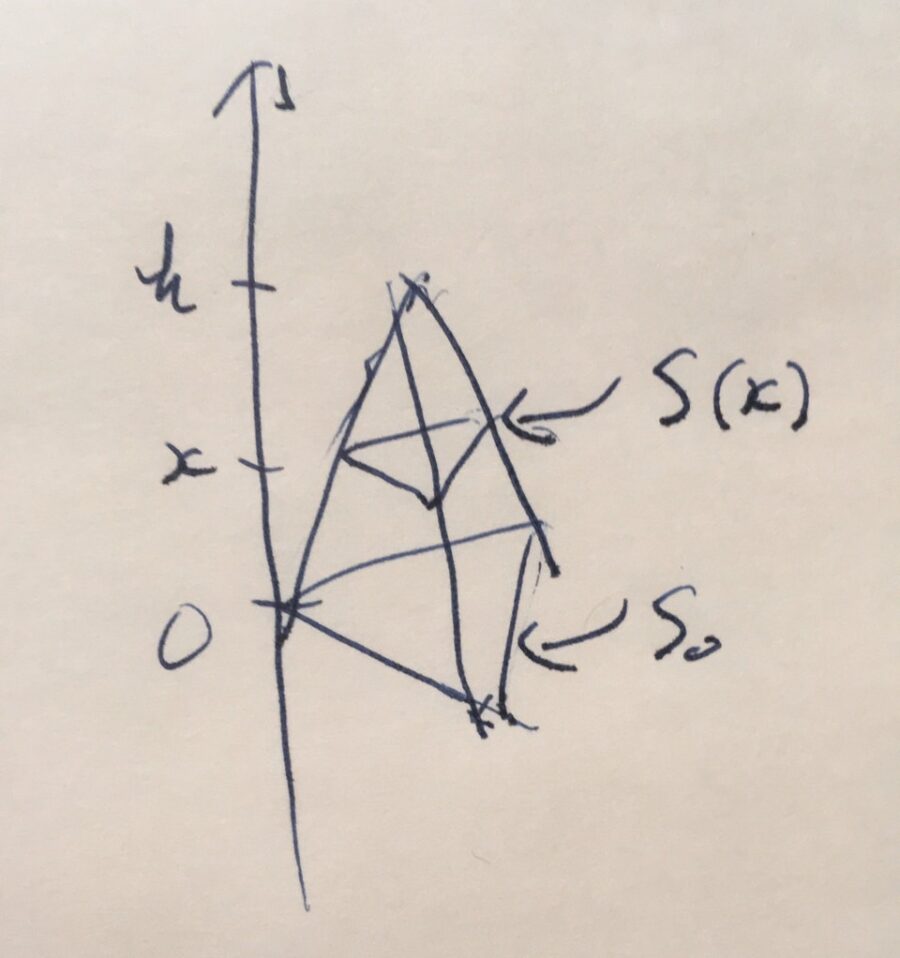
三角錐や四角錐などの角錐、円錐の体積\(V\)は、底面積を\(S_0\)、高さを\(h\)として
\[V = \frac{1}{3}S_0 h\]
となることを小中学校で学ぶでしょう。
特殊なケースでは、角柱を3つに分割して3つの角錐ができることによってそれを確かめることができます。
今回は一般的な証明をするために、高校で扱う積分を用いましょう。
上の図のように底面に垂直な方向に軸を取り、位置\(x\)における角錐・円錐の断面積を\(S(x)\)とします。
この断面積\(S(x)\)を、\(x=0\)から\(x=h\)まで細かく足しわせていったもの、すなわち積分が角錐・円錐の体積です。
\[V = \int_0 ^h S(x)dx\]
これを計算するために、\(S(x)\)を既知の数、\(S_0,h\)を使って表せないか考えます。
角錐・円錐においては、底面と断面は常に相似な図形となり、その辺の長さ・周長は高さに比例します。また、面積は相似比の2乗に比例するので、
\[\frac{S(x)}{S_0} = \frac{(h-x)^2}{h^2}\]
となります。したがって、
\[S(x) = \frac{(h-x)^2}{h^2} S_0\]
です。これと積分の一般的な計算式:\(\int x^2 dx= \frac{1}{3}x^3 +C\)を用いて積分を計算すれば、
\[\begin{aligned} V& = \int_0^h \frac{(h-x)^2}{h^2} S_0dx\\ &= \frac{S}{h^2}\int_0^h (h-x)^2dx \\&= \frac{S_0}{h^2}[-\frac{1}{3}(h-x)^3]_0 ^h \\&= \frac{S_0}{h^2}(0+\frac{1}{3}h^3)\\ &= \frac{1}{3}S_0 h\end{aligned}\]
と求めることができました。
おおざっぱに言えば、角錐や円錐の体積とは断面積の積分のことですが、断面積は高さの二乗に比例し、\(x^2\)の項が出てくるので、それを積分すると\(\frac{1}{3}x^3\)となる、ということですね。
以上、角錐・円錐の体積はなぜ1/3か:積分による証明をを紹介してきました。
面積や体積の公式は小中学校で学びますが、なぜそうなるのか理屈で納得するのはその段階では難しいかもしれません。興味を持ったら、ぜひ積分まで学んでみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)