どうも、木村(@kimu3_slime)です。
今回は、円周と直径の比が一定になるのはなぜか:円周率の三角関数による定義を紹介します。
円周率の素朴な定義
小中学校で円周率を学ぶときには、次のような説明がされるでしょう。
円の円周を\(C\)、直径を\(d\)とするとき、その比\(\frac{C}{d}\)を円周率と呼び、\(\pi\)という記号で表す。
言い換えれば、円周は直径の円周率倍である\(C =\pi d= 2\pi r\)。
この素朴な定義の前提には、次の事実があります。
どのような円を考えても、円周と直径の比は正の定数である。
小中学生向けの説明としては、実際に円をいくつか作ってその長さを測り、約3倍であることを体感するでしょう。
今回は、高校数学から大学教養程度の数学の知識を用いて、この事実をより基本的な立場、三角関数を使って説明していきましょう。
円周率の三角関数による定義
円周率をきちんと定義するには、円周という曲線の長さを定義しなければなりません。それを定義するために、三角関数と微分積分を用います。
まず、三角関数を「辺の長さの比、単位円」ではないやり方で定義します。
三角関数の微分を知っている立場からすると、それはテイラー展開
\[\cos x = \sum_{k=0}^\infty \frac{(-1)^k}{(2k)!}x^{2k}\]
\[\sin x = \sum_{k=0}^\infty \frac{(-1)^k}{(2k+1)!}x^{2k+1}\]
することができます。この事実を逆に出発点として、新たに三角関数を
\[\cos x := \sum_{k=0}^\infty \frac{(-1)^k}{(2k)!}x^{2k}\]
\[\sin x := \sum_{k=0}^\infty \frac{(-1)^k}{(2k+1)!}x^{2k+1}\]
という右辺のべき級数によって定義しましょう。これを三角関数のべき級数による定義と呼びます。
例えば、\(x=0\)のときを考えると、\(x^{0}=1\)の項のみが残って1次以降の項が消え、\(\cos 0 =1\)、\(\sin 0 =0\)を満たすことがわかりますね。
この級数は良い性質を持ち(絶対収束し)、\(\frac{d}{dx}(\cos x)= -\sin x\)、\(\frac{d}{dx}(\sin x)= -\cos x\)という微分の性質を満たします。
さて、この三角関数を用いれば、円周率が「曲線の長さ」を用いずに定義できます。
単位円による三角関数の定義では、コサインは
\[\cos \frac{\pi}{2}=0\]
を満たしました。逆に、べき級数による三角関数を採用し、
\[\cos \frac{x}{2}=0\]
を満たす\(0<x<4\)を円周率\(\pi\)として定義しましょう。
これを満たす\(x\)が存在することは、中間値の定理から証明することができます。詳しい議論は、杉浦「解析入門 Ⅰ」を参照してください。
他にも、この三角関数が周期性を持つこと、二乗の和が一定であること\((\cos x)^2+(\sin x)^2 =1\)、円周が\(c(t) = (r \cos t , r \sin t)\)とパラメータ表示できること、偏角\(\theta\)を用いて\(x=r\cos \theta, y =r \sin \theta\)と表せること(極座標表示)が証明できます。
(ちなみに、円周率の定義自体はべき級数による三角関数以外にも、さまざまなものがあります。半径1の円の面積として定義、アークタンジェントによる定義、積分による定義など。いずれにせよ、円周率は多項式による方程式の解とならない数:超越数であることが知られています。\(\cos \frac{x}{2}=0\)は、\(\cos\)がべき級数を表すので、「無限次」の多項式の方程式であり、極限を使って得られる数となっています。)
円周を求める
こうして定義した円周率が、円周と直径の長さの比となることを証明しましょう。
一般に、平面上の曲線\(c: [a,b]\to \mathbb{R^2}\)の長さは、
\[L = \int _{a}^{b} \|c^{\prime}(t)\|dt\]
によって定義されます(線積分)。
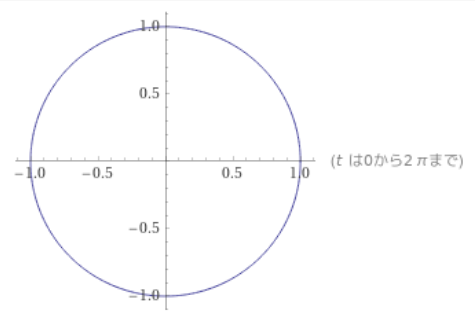
画像引用:WolframAlpha
半径\(r\)の円周という曲線は、\(c(t) = (r \cos t , r \sin t)\)、\(0 \leq t \leq 2 \pi\)と定義できます。すると、\(c^{\prime}(t) =(-r \sin t, r \cos t)\)であり、\(\|c^{\prime}(t)\|= \sqrt{r^2 (\sin t)^2+ r^2 (\cos t)^2} =r\)です。したがって、円周は
\[\begin{aligned} L&= \int _{0}^{2\pi} \|c^{\prime}(t)\|dt \\ &= \int _0^{2\pi} r dt \\&= 2 \pi r \end{aligned}\]
となりました。よって、円周と直径の比は
\[\frac{L}{d}= \frac{2\pi r}{2r} = \pi\]
と円周率になることが示せました。
以上、円周と直径の比が一定になるのはなぜか:円周率の三角関数による定義を紹介してきました。
「円周の長さとは何か」を深掘りし、三角関数をべき級数として定義すれば、比が一定となることが定理として証明できるわけですね。
円周と直径の比が一定になることは、経験則として捉えて良いと思いますが、厳密に議論したいならば三角関数や微積分の知識が必要となることが伝われば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)