どうも、木村(@kimu3_slime)です。
今回は、2本の平行線の距離が一定であることの証明を紹介します。
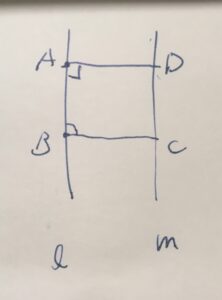
2本の平行線(交わらない直線)\(\ell,m\)があるとしましょう。1本の直線と点との距離(最短の線分)は、垂線となります。
この2本の平行線におけるどの2点を考えても、その距離は一定になります。
つまり、\(A,B\)を\(\ell\)上の任意の点、そこを通る垂線と\(m\)の交点を\(D,C\)とするとき、必ず\(AD =BC\)となります。
この性質は、平行線はどこにおいても等距離(equidistant)と呼ばれるものです。
証明していきましょう。
方針として、四角形\(ABCD\)が平行四辺形であることを示します。
まず\(\ell,m\)が平行なので、その一部分である\(AB,CD\)は平行です。
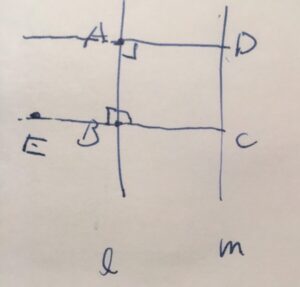
線分\(BC\)を伸ばし、\(B\)の外側の点を\(E\)としましょう。
\(AD,BC\)は垂線なので、\(\angle BAD =90^{\circ}\)、\(\angle ABE=90^{\circ}\)です。したがって、\(\angle BAD \angle ABE\)であり、2本の直線の錯角が等しいので、\(AD,BC\)は平行です。
よって、四角形\(ABCD\)は平行四辺形です。平行四辺形の向かい合う辺の長さは等しいので、\(AD=BC\)が示せました。
以上、2本の平行線の距離が一定であることの証明を紹介してきました。
交わらない直線の距離が一定であることは、見た目には明らかですが、どの点に注目しても平行四辺形ができるから、という理屈がわかるのは嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)