どうも、木村(@kimu3_slime)です。
今回は、平行四辺形の対角線によって合同な三角形ができることの証明を紹介します。
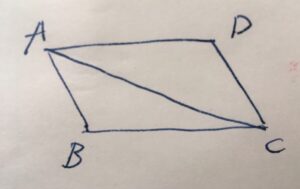
平行四辺形\(ABCD\)について、対角線\(AC\)があるとしましょう。
それによってできる2つの三角形\(\triangle ABC ,\triangle CDA\)は、合同になります。
対角線が\(BD\)であっても、同様の事実が成り立ちます。
では、証明していきましょう。
平行四辺形を考えているので、向かい合う辺\(AB,CD\)は平行です。2本の平行線とそれを横断する線分\(AC\)に注目すると、\(\angle BAC,\angle DCA\)は錯角の関係にあります。平行線の錯角の大きさは等しいので、\(\angle BAC=\angle DCA\)です。
同様に、\(BC,DA\)は平行です。錯角は等しいので、\(\angle ACB=\angle CAD\)となります
また、\(\triangle ABC ,\triangle CDA\)に共通する辺として、\(AC =CA\)です。
よって、三角形の合同条件、1組の辺の長さとその両端の角度が等しい(ASA)ので、\(\triangle ABC ,\triangle CDA\)が合同であることが示せました。
この結果からは、平行四辺形について次の性質がわかります。
- 平行四辺形の向かい合う辺の長さは等しい
- 平行四辺形の向かい合う角度は等しい
長さと角度が等しいことは、さきほど示した三角形の合同からわかります。
例えば角度は、\(\angle BAC=\angle DCA\)、\(\angle ACB=\angle CAD\)なので、足し合わせれば向かい合う角度が等しい\(\angle BAC+\angle CAD = \angle DCA+ \angle ACB\)です。
以上、平行四辺形の対角線によって合同な三角形ができることの証明を紹介してきました。
平行四辺形の対辺、対角が等しいという性質を引き出すために、対角線によって合同な三角形を見出す、という発想は面白いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)