どうも、木村(@kimu3_slime)です。
今回は、ユークリッド幾何における三角不等式の証明を紹介します。
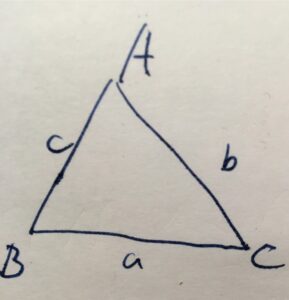
三角形の辺の長さ\(a,b,c\)について、常に2つの辺の長さの和は他の辺の長さより大きい
\[a < b+c\]
\[b < c+a\]
\[c < a+b\]
が成り立ちます。これは三角不等式(triangle inequality)と呼ばれるものです。
これらをまとめた条件
\[|a-b|< c<a+b\]
は、三角形の成立条件と呼ばれています。
今回は、「垂線が直線上の点と直線外のある点を結ぶ最短の線分」であることを前提に、三角不等式を証明していきます。
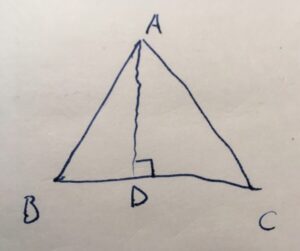
\(BC < AB +CA\)を示しましょう。
\(A\)を通り\(BC\)に垂直な線分を描き、\(BC\)との交点を\(D\)とします。
線分の長さを比較します。線分\(AD\)と点\(B\)に注目すると、\(BD\)が垂線なので最短であり、\(BD < AB\)です。
同様に、線分\(AD\)と点\(C\)に注目すると、\(CD\)が垂線なので最短であり、\(CD < CA\)です。
したがって、不等式は和を取っても成り立つことから、\(BD+CD <AB B+CA\)となります。
線分の分割と長さの関係(segment-addition postulate)から\(BD+CD=BC\)です。よって、三角不等式\(BC < AB +CA\)が示せました。
以上、ユークリッド幾何における三角不等式の証明を紹介してきました。
より一般に、ノルム(ベクトルの長さ)は
\[\|a+b\| \leq \|a\|+\|b\| \]
という三角不等式を満たすことが定義として要請されます。
その原型となる三角形の三角不等式ですが、垂線の最短性を用いると簡単に説明できるわけですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)