どうも、木村(@kimu3_slime)です。
今回は、二等辺三角形の底角が等しいこと、その逆の証明を紹介します。
二等辺三角形の底角が等しいこと
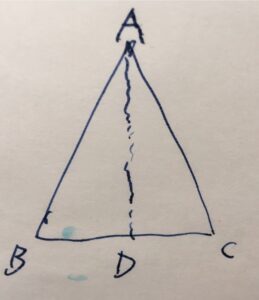
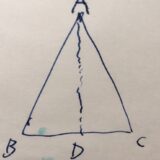
二等辺三角形\(\triangle ABC\)を考えましょう。長さが等しい辺を\(AB=AC\)とするとき、それらに隣接していない頂点による角\(\angle ABC , \angle ACB\)を底角(base angle)と呼びます。
このとき、必ず底角の角度は等しくなります \(\angle ABC = \angle ACB\) 。
証明していきましょう。
頂角\(\angle BAC\)の二等分線を考え、\(BC\)との交点を\(D\)とします。
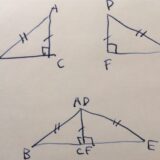
\(\angle BAD = \angle CAD\)であることから、\(\triangle BAD\)と\(\triangle CAD\)は合同になります。
したがって、その対応する角度は等しいです\(\angle ABD = \angle ACD\)。同一の角度として表記を変えれば、\(\angle ABC = \angle ACB\)が示せました。
2つの角が等しい三角形は二等辺三角形
この性質は、逆が成り立ちます。
つまり、もし2つの角度が等しい三角形があるならば、それは必ず二等辺三角形です。

\(\triangle ABC\)において、\(\angle ABC = \angle ACB\)と仮定しましょう。
頂角\(\angle BAC\)の二等分線を考え、\(BC\)との交点を\(D\)とします。
二等分線であることから、\(\angle BAD = \angle CAD\)です。また、三角形の内角の和は180度であることから、
\[\angle BAD +\angle ABD +\angle ADB=180^\circ\]
\[\angle CAD +\angle ACD +\angle ADC=180^\circ\]
です。仮定より\(\angle ABD = \angle ACD\)なので、\(\angle ADB= \angle ADC\)が導けます。また、共通する辺として、\(AD= AD\)です。
よって、三角形の合同条件、1組の辺とその両端の角度が等しい(ASA)から、\(\triangle ABD = \triangle ACD\)となります。
特に、対応する辺の長さは等しいので、\(AB=AC\)、つまり二等辺三角形となることが示せました。
正三角形と内角の関係
今回の結果を正三角形のケースに当てはめると、次のことが言えます。
- 3つの辺の長さが等しい(正三角形)ならば、3つの内角は等しい。特にそれぞれ\(\frac{180}{3}^{\circ}= 60^{\circ}\)となる。
- 逆に、三角形の3つの内角の大きさが等しい、それぞれ\(\frac{180}{3}^{\circ}= 60^{\circ}\)ならば、その3つの辺の長さは等しい(正三角形である)。
3つの辺の長さが等しい三角形は、複数の見方で二等辺三角形として見ることができます。したがって、底角の大きさが等しいという事実から、3つの角の大きさが等しいと導けるわけです。
3つの辺の長さが等しい三角形を等辺三角形(equilateral triangle)、3つの角度が等しい三角形を等角三角形(equiangular triangle)と呼びましょう。
この言葉を使ってまとめれば、三角形について、等辺三角形であることと、等角三角形であることは同値です。
以上、二等辺三角形の底角が等しいこと、その逆の証明を紹介してきました。
角度や長さが等しいことを示すために合同の性質に持ち込むわけですが、二等辺三角形の場合は、頂角の二等分線を考えると合同な三角形ができるのがポイントですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)
こちらもおすすめ
二等辺三角形の頂角の二等分線によってできる三角形は合同であることの証明
三角形の内角の和が180度であることの証明:補助線、平行線公準を用いて