どうも、木村(@kimu3_slime)です。
今回は、双曲幾何学入門ということで、平行な直線が無限に存在することについて紹介します。
上半平面における直線
平面の上半分、上半平面\(\mathbb{H} := \{(x,y)\in \mathbb{R}^2 \mid y>0\}\)を舞台としましょう。
ここで、ユークリッド幾何学で考える直線とは異なる「直線」を導入します。
- タイプ1の直線(type I line)
- \[\{(x,y) \in \mathbb{H} \mid x =a\}\]
- タイプ2の直線(type II line)
- \[\{(x,y) \in \mathbb{H} \mid (x-c)^2+y^2 =r^2\}\]
つまり、\(y\)軸に平行な直線か、\(x\)軸上に中心を持つ円を\(\mathbb{H}\)における直線と呼びます。

例えば、
\[\{(x,y) \in \mathbb{H} \mid x =1\}\]
\[\{(x,y) \in \mathbb{H} \mid (x-1)^2+y^2 =\frac{4}{9}\}\]
\[\{(x,y) \in \mathbb{H} \mid (x+\frac{3}{2})^2+y^2 =\frac{1}{4}\}\]
は\(\mathbb{H}\)における直線の定義を満たします。
(実は、これらの「直線」は、特殊な「距離」での最短距離を実現する曲線:測地線になることが知られています。その意味でも、直線であるわけです。)
このように直線を定義すると、\(\mathbb{H}\)の異なる2点を通る直線が存在することが示せます。
一般に、舞台となる集合と(一定の条件を満たした)「直線」の組を、抽象幾何(abstract geometry)と呼びます。
今回考えた上半平面と直線の組\((\mathbb{H}, \mathcal{L})\)は、抽象幾何の定義を満たします。特に、ポアンカレの上半平面モデル(Poincaré half-plane model)と呼ばれ、双曲幾何学(hyperbolic geometry)と呼ばれるものの一種です。
ユークリッド幾何学では、異なる2点を通る直線はただひとつでした。こうした条件を満たす幾何学は、結合幾何(incidence geometry)と呼ばれます。
上半平面モデルにおいても、異なる2点を通る直線はただひとつ存在することが知られています。
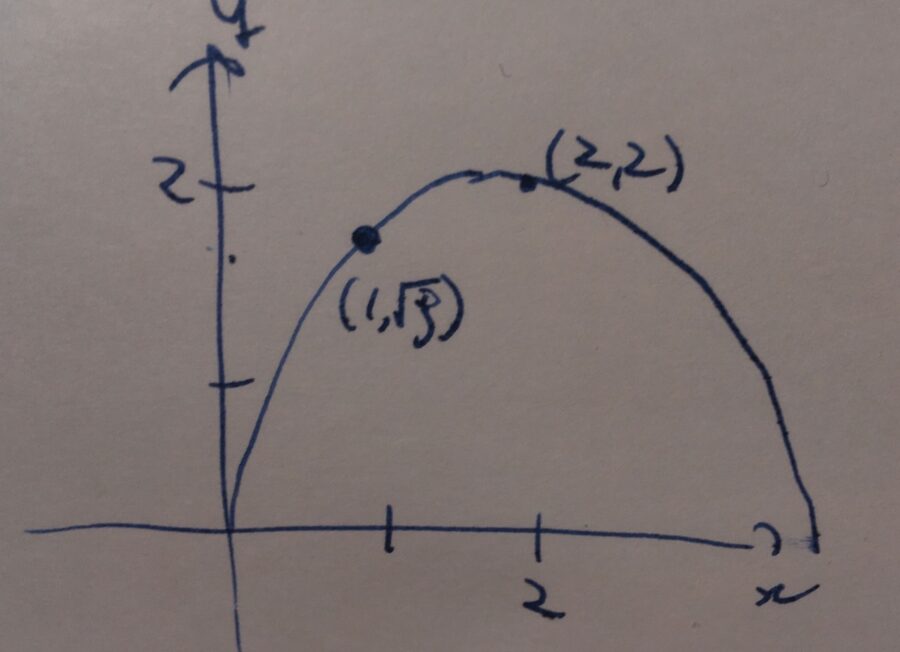
例えば、\((1,\sqrt{3})\)と\((2,2)\)を通る直線は、\((x-2)^2+y^2 = 2^2\)です。
2点の\(x\)座標が異なるとき、それはタイプ2の直線となりますが、\((x-c)^2+y^2 =r^2\}\)と2点を通るという情報から、2つのパラメータ:中心の\(x\)座標と半径\(c,r\)が1つに決まるわけです。
一般に、3点を通る円はただひとつに決まりますが、今回は中心の\(y\)座標を0に固定しているので、2点で決まっています。
平行線が無限に存在すること
ユークリッド幾何学と双曲幾何学の違いとしては、平行線の公準の話が有名です。
ユークリッド幾何学においては、直線とその直線上にない点があるとき、その点を通りその直線に平行な直線が存在します。これは議論の出発点、平行線の公準と呼ばれるものです。これはユークリッド幾何学において、他の公理から証明できないものとして知られています。
上半平面モデルにおいては、直線上にない点を通る平行な直線は無限に存在します。2つの直線が平行とは、それらが交わらない(共通部分を持たない)ことです。
例えば、
\[\{(x,y) \in \mathbb{H} \mid x=0\}\]
という直線を考えましょう。そして、例えば直線上にない点\((1,1)\)を考えます。
そこを通る平行な直線は、\(x=1\)だけではありません。
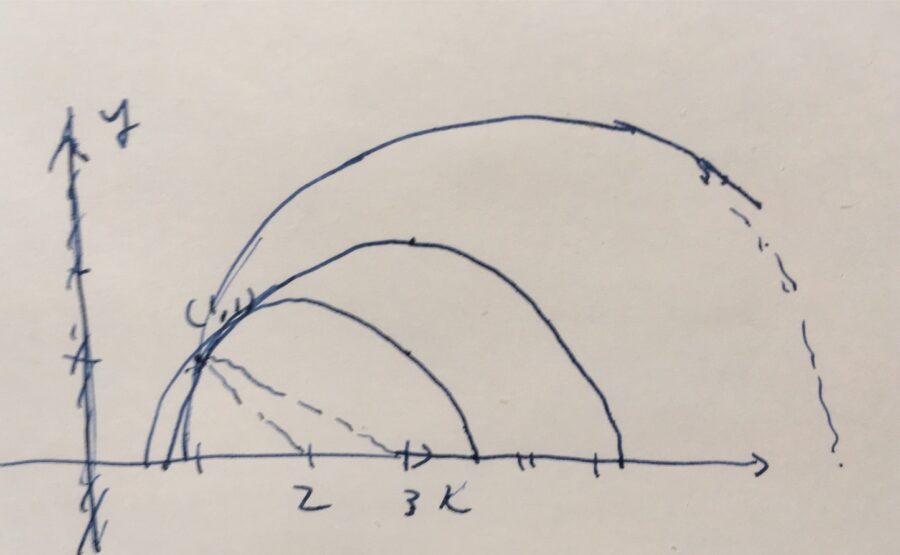
その点を通る直線として、
\[\{(x,y) \in \mathbb{H} \mid (x-2)^2 +y^2 = (\sqrt{2})^2\}\]
\[\{(x,y) \in \mathbb{H} \mid (x-3)^2 +y^2 =(\sqrt{5})^2\}\]
\[\{(x,y) \in \mathbb{H} \mid (x-a)^2 +y^2 =(\sqrt{1+(a-1)^2})^2\}\]
(\(a>1\))など、無限に考えることができます。そしてこれらはどれも、\(x=0\)とは交わらず、平行です。
他に、タイプ2の直線を基準にしても、同様にして内側または外側の点を通る無数の円を考えることができます。
このようにして、直線上にない点を通る平行な直線が無限に存在することが示せます。
以上、双曲幾何学入門ということで、平行な直線が無限に存在することについて紹介してきました。
球面における幾何学とも比較すると、「常に平行線が1本引ける」というユークリッド幾何学の「当たり前」が、当たり前でなかったことがわかりますね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)
Geometry: A Metric Approach with Models (Undergraduate Texts in Mathematics)
Springer (1990-12-17T00:00:01Z)
¥4,065 (中古品)
こちらもおすすめ
三角形の内角の和が180度であることの証明:補助線、平行線公準を用いて