垂直な直線の定義、直角に交わることの証明

どうも、木村（@kimu3_slime）です。

「垂直な直線とは何か」と聞かれたら、「直角（90度）で交わる直線だ」と答える人が多いのではないのでしょうか。実際、それは正しいです。

しかし、垂直な直線には「隣り合う角の大きさが等しくなるような直線」という定義もあります。今回はそこから、直角に交わることを性質として証明してみましょう。

直線\(\ell , m\)があり、それらが垂直である\(\ell \perp m\)としましょう。また、直線上の点を次の図のように、\(A,B,C,D,E\)とします。

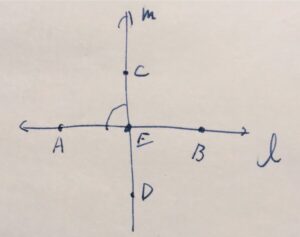
このとき、\(\angle AEC\)が直角であることを証明します。

垂直な直線の定義、隣り合う角の大きさが等しくなることから、\(\angle AEC= \angle CEB\)です。

\(\angle AEB\)に注目すると、\(A,E,B\)は同じ直線\(\ell\)上の点なので、直線のなす角度の定義から\(\angle AEB = 180 ^{\circ}\)です。

また、点\(C\)は角\(\angle AEB\)の内側にあるので、それは2つの角度に分けられます \(\angle AEB = \angle AEC + \angle CEB\) （angle addition postulate）。

以上の結果をまとめれば、\(2 \times \angle AEC = 180^{\circ}\)です。2で割れば、\(\angle AEC = 90 ^{\circ}\)、つまり\(\angle AEC\)が直角であることが示せました。

この証明は、当然\(\angle BEC\)が直角であることも示していますね。

全く同様にして、\(\angle AED\)や\(\angle BED\)も直角であることが示せます。

逆に、「垂直な直線とは直角で交わる直線」を定義として出発して、「隣り合う角の大きさが等しい」を性質として導くこともできますね。

ちなみに垂直と直角という用語の違いですが、垂直は（2つの）直線の状態を表す言葉で、直角は角の大きさ（角度）を表す言葉です。直線が直角、角が垂直とは言わないわけですね。

以上、垂直な直線の定義、直角に交わることの証明を紹介してきました。

垂直な直線とは「それによってできる隣り合う角の大きさが等しくなる直線」という立場から出発すれば、その角度は直線の二等分、つまり直角になるというわけです。90度で交わる直線というだけでなく、隣り合う角度が等しくなる直線としても見れると面白いですね。

木村すらいむ（@kimu3_slime）でした。ではでは。

posted with AmaQuick at 2022.05.16

()

￥13,970 (中古品)

こちらもおすすめ