どうも、木村(@kimu3_slime)です。
ユークリッド幾何学における議論の出発点、公準のひとつに、次のようなものがあります。
もし異なる平面が交わる(共通部分を持つ)ならば、その共通部分は直線である
今回はそれについて、線形代数による説明をします。
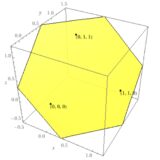
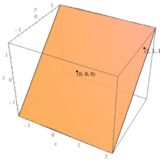
3次元の空間\(\mathbb{R}^3\)において、\(z=y\)により定まる平面と、\(y=0\)により定まる平面を考えましょう。
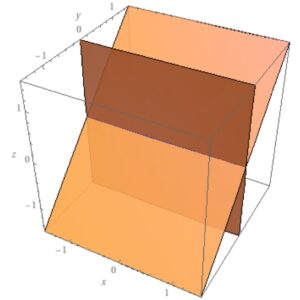
画像引用:WolframAlpha
これらの平面は共通部分を持ちます。具体的には、\(z=y=0\)を満たす点の集まり、\(x\)軸(\(\{(x,0,0) \mid x \in \mathbb{R}\}\))がその共通部分です。確かにそれは直線ですね。
2つの平面が交わらないときは、それらの平面は平行であると呼ばれます。
より一般的に、座標、線形代数の枠組みを使って考えていきましょう。
2つの平面が交わるとき、その交わる点のひとつを原点とします。
つまり、\(V= \mathbb{R}^3\)において、2つの平面(2次元の部分線形空間)\(W_1 ,W_2\)があり、共通部分を持つとしましょう。これらの平面は平行でないことから、2つは完全には一致しない、\(W_1 \neq W_2\)です。
一般に、部分線形空間の和空間と共通部分はまた部分線形空間となり、
\[ \begin{aligned}&\dim(W_1+W_2)\\&=\dim W_1 +\dim W_2 -\dim (W_1 \cap W_2)\end{aligned} \]
という次元に関する等式が成り立ちます。
\(W_1,W_2\)が平面であることから、\(\dim W_1 =2\)、\(\dim W_2 = 2\)です。
また、\(W_1 \neq W_2\)であることから、\(W_2\)は\(W_1\)の基底に対して線形独立なベクトルを含んでいます。したがって、和空間の次元は\(\dim(W_1+W_2) =3\)です。異なる平面上のベクトルを組み合わせれば、空間内のすべてのベクトルが表現できます。
よって、
\[ \begin{aligned} & \dim (W_1 \cap W_2)\\ &=\dim W_1 +\dim W_2 – \dim(W_1+W_2) \\ &= 1 \end{aligned} \]
となるので、共通部分\(W_1 \cap W_2\)は1次元の部分線形空間、すなわち直線となることが示せました。
以上、交わる平面の共通部分が直線であることにについて、線形代数による説明をしてきました。
平面が交わると直線ができることは当たり前に見えますが、それを線形代数の立場から証明できることが伝われば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)