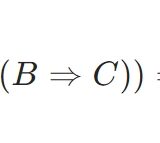複数の命題の同値「A⇔B⇔C」はサイクル「A⇒B⇒C⇒A」と同値であることの証明

どうも、木村（@kimu3_slime）です。

今回は、複数の命題の同値「A⇔B⇔C」は、サイクル「A⇒B⇒C⇒A」と同値であることの証明を紹介します。

前提知識：記号論理、命題論理入門：覚えるべき論理記号（否定、かつ、または、ならば、同値）とは

示したいことは、命題\(P,Q\)を

\[P : A \Leftrightarrow B \Leftrightarrow C\]

\[Q : A \Rightarrow B\Rightarrow C \Rightarrow A\]

とするとき、\(P\)と\(Q\)が同値であることです。

論理的に同値であることの定義を確認すると、\(P\Leftrightarrow Q\)とは、「\(P \Rightarrow Q\)かつ\(Q \Rightarrow P\)」が成り立つことです。

また、\(P,Q\)の表現では略記を用いています。「\(A \Leftrightarrow B \Leftrightarrow C\)」とは、「\(A \Leftrightarrow B\) かつ \(B \Leftrightarrow C\)」のことです。「\(A \Rightarrow B\Rightarrow C \Rightarrow A\)」とは、「\(A\Rightarrow B\)かつ\(B\Rightarrow C\)かつ\(C\Rightarrow A\)」のことです。

まず、\(P\)を仮定して\(Q\)が成り立つことを示しましょう。

仮定より\(A\Leftrightarrow B\)なので、論理同値の定義から\(A\Rightarrow B\)が成りたちます。また、仮定より\(B\Leftrightarrow C\)なので、\(B \Rightarrow C\)が成りたちます。

さらに、\(A\Leftrightarrow B\)かつ\(B\Leftrightarrow C\)なので、特に\(C \Rightarrow B\)と\(B \Rightarrow A\)が成り立っています。したがって、論理の基本法則（「ならば」の推移律）から、\(C \Rightarrow B\)が成りたちます。

以上をまとめれば、「\(A\Rightarrow B\)かつ\(B\Rightarrow C\)かつ\(C\Rightarrow A\)」が成り立つこと、\(Q\)が成り立つことが示せました。

逆に、\(Q\)を仮定して\(P\)が成り立つことを示します。

仮定より\(A \Rightarrow B\Rightarrow C\)が成り立つので、残すのは逆向きの論理です。

仮定より\(C \Rightarrow A\)かつ\(A\Rightarrow B\)が成り立つので、推移律から\(C \Rightarrow B\)です。同様に、\(B \Rightarrow C\)かつ\(C\Rightarrow A\)が成り立つので、推移律から\(B \Rightarrow A\)です。つまり、\(C \Rightarrow B\Rightarrow A\)が成りたちます。

以上をまとめると、「\(A \Leftrightarrow B\) かつ \(B \Leftrightarrow C\)」、すなわち\(P\)が成り立つことが示せました。

よって、「\(P \Rightarrow Q\)かつ\(Q \Rightarrow P\)」が成り立つことが示せたので、\(P,Q\)は論理的に同値です。

以上、複数の命題の同値「A⇔B⇔C」は、サイクル「A⇒B⇒C⇒A」と同値であることの証明を紹介してきました。

今回は3つの命題を題材としていますが、4つ以上でも同様の議論が成りたちます。

数学では、しばしば複数の命題の同値性を示したい場面がありますが、相互に同値であることを示すのは手間がかかります。そこで循環的に成り立つことを示せば十分である、とわかれば便利です。

例えば、杉浦「解析入門 Ⅰ」では、実数の公理の同値性を示すためにこの論法を用いています。