どうも、木村(@kimu3_slime)です。
小学校の算数の時間では、ゼロ0という数について学びます。
ゼロは整数1,2,3などに比べて、後になって発見(発明)されたものです。
名著とされる吉田洋一氏の『零の発見』(岩波新書 1939年)によれば、零の発見されたのはインドにおいてであった。6世紀頃に位取り記数法が行われるようになり、7世紀初めごろのインドの数学者ブラーマグプタの書物には、「いかなる数に零を乗じても結果は常に零であること」、また、「いかなる数に零を加減してもその数の値に変化がおこらないこと」という零の性質が記載されているという。
なぜゼロという数を考えるのでしょうか? 現代の立場から、僕なりに考えたメリットを簡単に紹介していきます。
巨大な数、小さな数を表すための0
ゼロの発見として有名な話では、何もない位を持つ数の区別があります。
六十進法を用いたバビロニアの数の表記には、古くは 0 がなく、例えば「62」と「602」は表記が全く同じで、見分けがつかなかった。これは非常に不便であったので、時代が下ると 6 と 2 の間に斜めの楔を並べて、62 と 602 の区別を表すようになった。この文字が人類が最初に 0 を表現した記号とされている
アラビア文字ではありますが、「\(62\)」という文字列が、六百二か六十二、はたまた六千二十のどれを意味しているのかわからなかったら、不便ですね。
位取り記数法(10進数)を使って数を表すときには、各位の数を並べて書いただけでは区別ができない数が生まれるので、空白の位を表す何らかの記号が必要になってくるでしょう。
しかし例えば漢数字で言えば、六百二と六十二は区別された表現になっています。これではゼロは必要ないのではない、と思うかもしれません。
僕としては、数の大きさを視覚的に区別するために、ゼロが役に立つと考えています。
| 十 | \(10\) |
| 百 | \(100\) |
| 千 | \(1000\) |
| 万 | \(10000\) |
| 十万 | \(100000\) |
漢数字の表記では、十倍された数の文字同士の関連性がありません。百を十個集めたものは千で、千を十個集めたものは万、と覚えるしかないでしょう。
ゼロを使った表現だと、\(100\)を\(10\)個集めたのが\(1000\)、\(1000\)を\(10\)個集めたものが\(10000\)となっていて、規則性がわかりやすくなっていますね。
さらにゼロを用いた表現の優れた点は、この議論をいくらでも拡張できるということです。巨大な数の表現に役立ちます。
兆、京、垓といった単位(名前)は、増えるほど覚えるのが大変ですし、命名の種類にも限界があります(例えば無量大数)。
\(0\)を使って表現すれば、\(1\)の後に\(0\)が68個並んだ数(\(10^{68}\))と説明できるわけです。この考え方は、10のべき乗を使って数を表す指数記法につながってきます。
参考:近似値を正確に:指数記法と有効数字、丸めとは何か、10のべき乗、マイナス乗:0の個数、小数表記の換算表
ごく小さな数の表現にも、ゼロは役に立ちます。
六割二厘といった位に応じた単位を用いたり、「小数点以下六百二」と表現することなく、\(0.602\)と表記すれば一目瞭然ですね。
位同士の計算を簡単にする0
さてここまでは位を表す記号としての0を見てきましたが、0同士の計算も大事で、それこそがゼロの発明と言われる側面です。
0という数が持つ性質として、0に何を足しても変わらない、0に何をかけても0があります。
\[0+x =0\]
\[0\times x =0\]
なぜこんな性質を持つ数を考えるのでしょうか? それは位同士の数の計算、筆算を便利にしてくれるものです。
例えば\(602+ 17\)について考えましょう。

0を用いることで、位同士の計算が自然とできるようになっています。そして10の位の計算では、\(0+1=1\)という計算をしていますね。何もない位を\(0\)で表し、足すときにはその位に影響しないようにすることが、\(0+x=x\)の利用法です。
比較として漢数字の表記を書きましたが、六百二という表記では十の位が表示されていません。十の位同士を意識して計算しようとすれば、ゼロ十と表すことになり、結果的にアラビア数字の考え方が持ち込まれることになりますね。
掛け算についても同様です。\(602 \times 2\)を計算してみましょう。
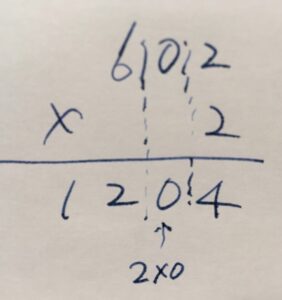
10の位の計算では、\(0 \times 2=0\)という計算をしています。これは何もない位(ゼロ十)が2つあっても0のままということで、そうした計算を表現しているのが\(0\times x =0\)ですね。
以上、ゼロ0をなぜ学ぶのかについて、巨大・微小な数の表現、位同士の計算への応用を紹介してきました。
慣れてしまった身としては、位取り表記やアラビア数字、ゼロの利用は当たり前に見えますが、具体的にゼロを利用している場面を考えると、やはり便利な発明だと感じますね。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1979-04-20T00:00:01Z)
¥836



