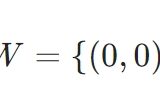点に大きさがないとは：ルベーグ測度による説明

どうも、木村（@kimu3_slime）です。

中学校で学ぶ幾何学、ユークリッド幾何学では、「点」は未定義語であり、位置を示すが大きさを持たないものとして説明されます。

今回は、点が大きさを持たないことの説明のひとつとして、そのルベーグ測度による大きさが0であることを紹介します。

ルベーグ測度とは、長さ、面積、体積といったものを一般化した関数のことです。

1次元のルベーグ測度\(\mu\)は、

\[\mu((a,b]) = b-a\]

を満たします。例えば、半開区間\((0,1] =\{x \mid 0< x \leq 1\}\)の測度（長さ）は\(\mu ((0,1])= 1-0 =1\)です。

ルベーグ測度は、上で示した条件と、一般的な測度の定義

空集合の測度は0：\(\mu (\varnothing) =0\)
非負性：すべての\(A \in \mathcal{B}(\mathbb{R})\)に対し\(\mu (A) \geq 0\)
加算加法性：すべての\((A_n)_{n \geq 0}\in \mathcal{B}(\mathbb{R})\)に対し、\(A_0 = \sum_{n\geq 1}A_n\)（共通部分を持たない和）ならば、\(\mu (A_0) = \sum_{n \geq 1}\mu(A_n)\)

を満たします。

要素を持たない集合の「大きさ」は0、「大きさ」は必ず0以上、「大きさ」は共通部分を持たない和に分割して計算できる、といったイメージです。

\(\mathcal{B}(\mathbb{R})\)は1次元のボレル集合体と呼ばれるもので、半開区間などをすべて含んでいます。「測れる」集合全体のことで、今回の議論では細かく気にしなくて良いでしょう。

ここまでの準備を用いれば、\(a\)を実数として、一点集合\(A = \{a\}\)が大きさを持たないこと、1次元ルベーグ測度で\(\mu (A)=0\)となることが示せます。

一点\(a\)を含む区間列として、\(A_n = (a-\frac{1}{n},a]\)を考えましょう。

\(A \subset A_n\)なので、測度の単調性から

\[\begin{aligned} \mu(A) &\leq \mu(A_n) \\&= \mu((a-\frac{1}{n}, a]) \\&= \frac{1}{n} \end{aligned}\]

となります。また、測度の非負性から\(\mu(A) \geq 0\)です。よって、両辺で\(n \to \infty\)の極限を取れば、\(\lim_{n\to \infty}\frac{1}{n} =0\)なので、はさみうちの原理から

\[\mu (A)=0\]

となることが示せました。

今回は簡単のために1次元ルベーグ測度（長さ）を考えましたが、2次元（面積）や3次元（体積）、一般的な次元のルベーグ測度においても、一点集合の測度（大きさ）は0となります。

以上、点が大きさを持たないことの説明のひとつとして、そのルベーグ測度による大きさが0であることを紹介してきました。