どうも、木村(@kimu3_slime)です。
Twitter上で、DNAの対数螺旋は三角関数によって表現できるという話を知りました。
三角関数といえば、昔授業で「身近にある三角関数を探してみよう」ってのをやったとき、
1人が「DNAの螺旋」って答えて「あれ、そうだっけ」って調べてみると、螺旋構造って真上から見たら円の形で真横から見たら三角関数の形ってことに気付かされた話を思い出した。DNAレベルから生き物は三角関数(?)— 横山 明日希 (@asunokibou) May 18, 2022
実際その通りだと思ったので、今回はその三角関数による表現についてグラフとともに紹介します。
生き物の細胞には核があり、その中にあるDNA(デオキシリボ核酸)には、遺伝情報が蓄えられています。
分子モデルは次の図のような形で、この構造は二重らせん構造(double helix)と呼ばれるものです。
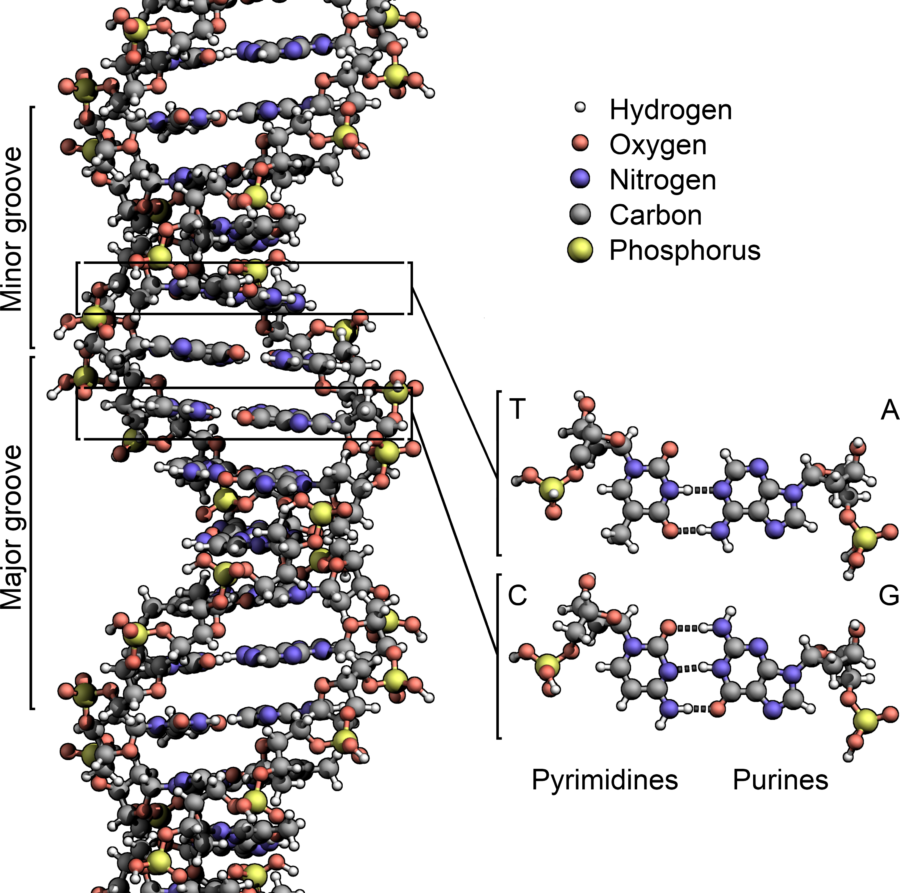
画像引用:Zephyris – Wikipedia
二重らせんに注目し、それを2つの空間曲線として数学的に表してみましょう。
まず、3次元空間\((x,y,z)\)におけるらせんは、
\[c_1 (t) = (\cos t ,\sin t, t)\]
と表せます。
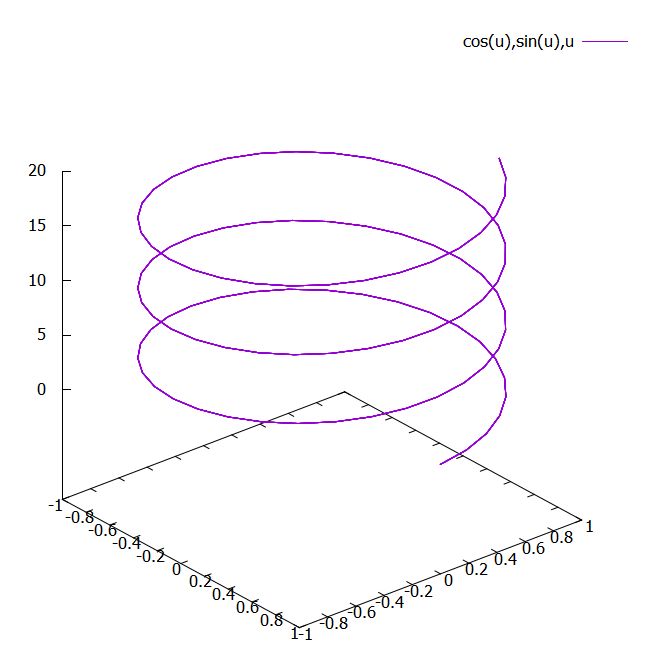
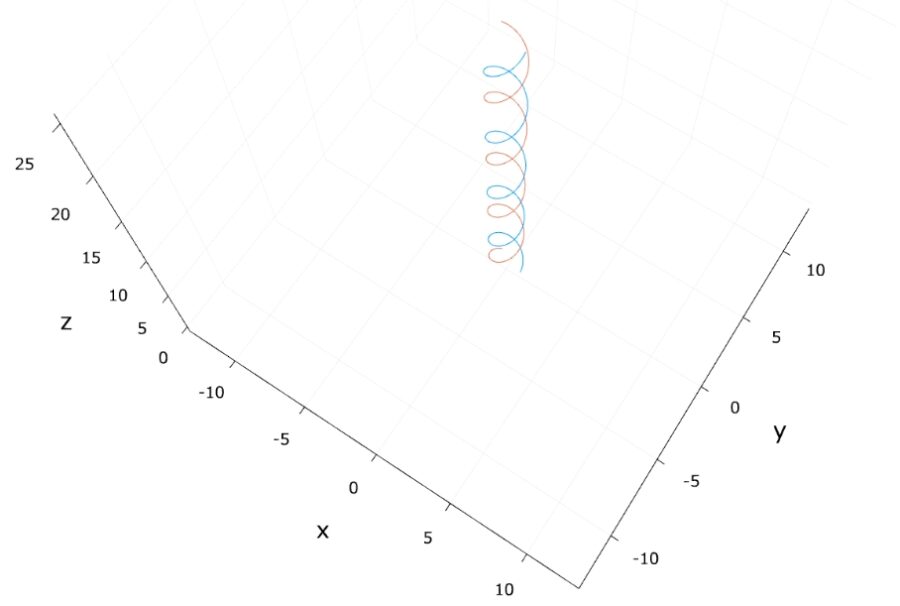
DNAにかぎらず、バネ、螺旋階段やスパイラルチューブのようならせんは、真横から見ると三角関数の形をしています。
ケーブルプロテクター ケーブル収納カバー ツイスト カラー TPU素材 断線防止 折り防止 汚れ防止 耐摩耗性 DIY 2 色 24セット 3.7cm (黒と白)
レモンツリー ()
¥607
ひとつのらせん\(c_1\)と、位相を\(\theta\)だけずらしたらせん
\[c_2 (t) = (\cos (t+\theta) ,\sin (t+\theta), t)\]
を合わせて描いてみましょう。
\(\theta = \pi\)のときは、次の通りです。
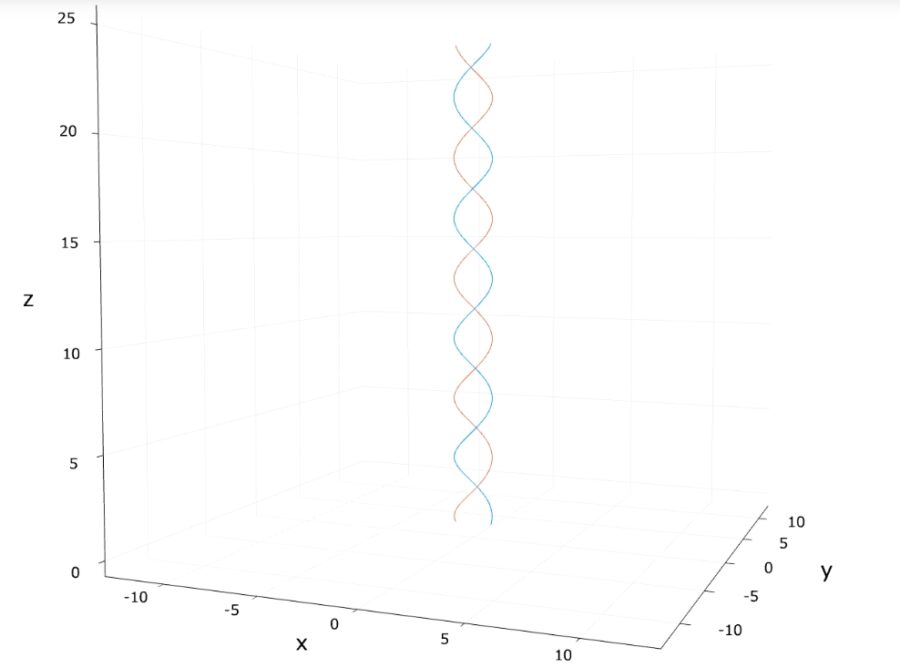
二重らせんらしい形が表現できていますね。
ただし、少しきれいすぎるようにも見えます。
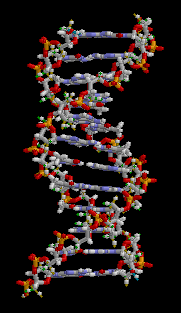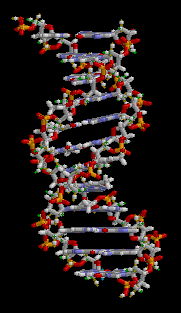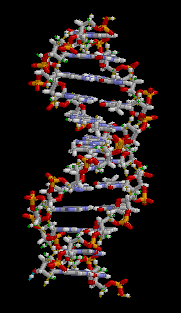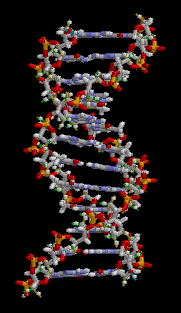
画像引用:brian0918™ – Wikipedia
このアニメーションと見比べてみると、2つのらせんの山は完全に反対の周期になっているわけではなく、山と山同士はやや近いですね(主溝と副溝)。
そこで位相のずれを\(\theta = \frac{3}{4} \pi \)としたときの図が次のものです。
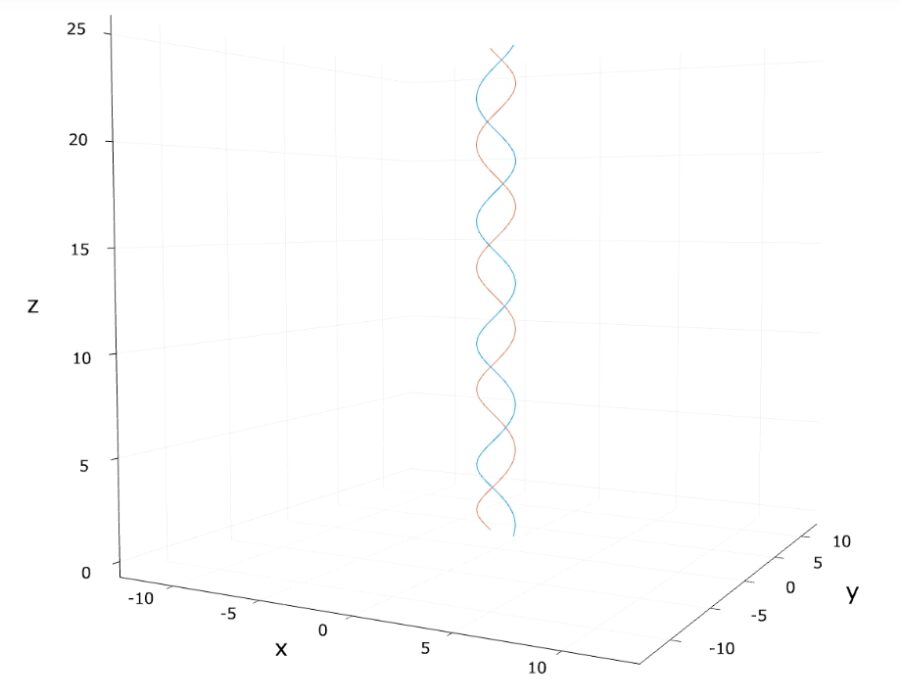
少しのいびつさがあり、DNAの二重らせんらしさが表現できました。
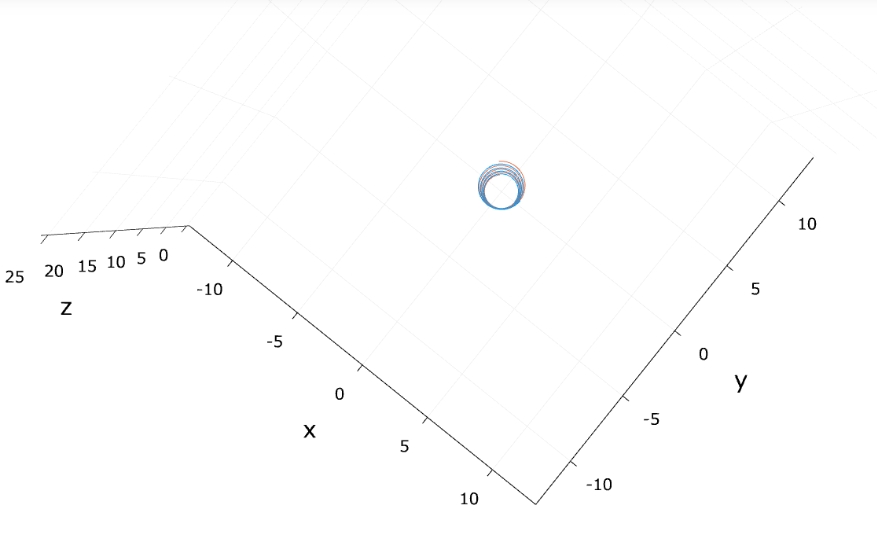
以上、DNAの二重らせんの三角関数による表現について紹介してきました。
僕は生物学が専門ではありません。DNAの構造が三角関数による螺旋で正確に表せるのか、位相のずれは\(\theta = \frac{3}{4} \pi\)が妥当なのかについては、検証されていないことに注意してしてください。
それでも、三角関数を使うと、DNAのような二重らせんがシンプルに表現できることが伝われば嬉しいえす。
木村すらいむ(@kimu3_slime)でした。ではでは。
改訂版 日本一詳しい 大学入試完全網羅 生物基礎・生物のすべて
KADOKAWA (2019-03-20T00:00:00.000Z)
¥2,574
数研出版 (2017-02-09T00:00:01Z)
¥2,486 (コレクター商品)
講談社 (1986-03-10T00:00:01Z)
¥1,500 (コレクター商品)
紀伊國屋書店 (2018-02-15T00:00:01Z)
¥2,970
こちらもおすすめ
Julia(SymPy)でパラメータ付けられた曲線(平面、空間)を描く方法