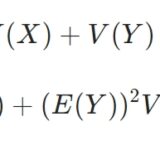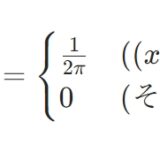どうも、木村(@kimu3_slime)です。
今回は、中心極限定理とは何か、Juliaでの計算例、その意味を紹介します。
中心極限定理
確率論や統計学において重要な定理として、大数の法則があります。それは、試行回数を増やすほど、サンプルの平均値が理論的な平均値に近づいていくというものでした。例えば、公平なコインをたくさん投げると、表が出る回数の平均はやがて\(\frac{1}{2}\)に近づいていきます。
ただし、サンプルの平均と理論的な平均を比べると、実際には誤差があります。その平均同士の誤差の分布が正規分布に従うことを述べるのが、中心極限定理(CLT; central limit theorem)です。
より精密に述べましょう。
\(X\)という確率変数(母集団分布)を考え、\(X\)の平均を\(\mu\)、分散を\(\sigma ^2\)としましょう。平均と分散は有限の値として存在し、分散は正であると仮定します。
\(X_1,\dots ,X_n\)をそのサンプル(独立で同分布な確率変数族, i.i.d.)とします。サンプルの平均は
\[M_n = \frac{X_1+\cdots +X_n}{n} \]
で、サンプルと理論平均の誤差を標準化した
\[Z_n = \frac{M_n -\mu}{\frac{\sigma}{\sqrt{n}}}\]
という確率変数(平均誤差)を考えましょう。このとき、\(n\)が大きくなるほど、平均誤差\(Z_n\)は標準正規分布Normal(0,1)に近づきます。
\[ \lim_{n \to \infty}Z_n = \mathrm{Normal}(0,1)\]
この収束の意味は、それぞれの累積分布関数が収束するということです(分布収束)。つまり、すべての\(x \in \mathbb{R}\)について
\[\lim_{n\to \infty} P(Z_n \leq x) = \Phi (x)\]
が成り立つという意味です。ただし、\(\Phi\)は標準正規分布の累積分布関数です。
標準化をもとに戻せば、サンプル平均\(M_n\)は次のように近似できるということです。
\[M_n \sim \mathrm{Normal}(\mu , \frac{\sigma^2}{n}) \]
サンプルの和\(S_n\)については、\(S_n = nM_n\)なので、
\[S_n \sim \mathrm{Normal}(n\mu , n\sigma^2)\]
と近似できます。
どんな分布に対するサンプルでも、その平均や和については正規分布で近似できる、というのが中心極限定理です。
Juliaで中心極限定理を試す
では、コンピュータ(Julia)で中心極限定理が何を言っているのか、実験してみましょう。
準備
Distributions、StatsPlotsを使うので、持っていないならばインストールしておきましょう。
1 2 3 | using Pkg Pkg.add("Distributions") Pkg.add("StatsPlots") |
準備として、以下を実行しておきます。
1 | using Distributions,StatsPlots, Random |
一様分布
離散一様分布DIscreteUniform(1,6)について試してみましょう。
ランダムなサンプルは「rand(分布,n)」で手に入れられます。
1 2 3 4 | d1 = DiscreteUniform(1,6) Random.seed!(2022) x = rand(d1,1000) histogram(x) |
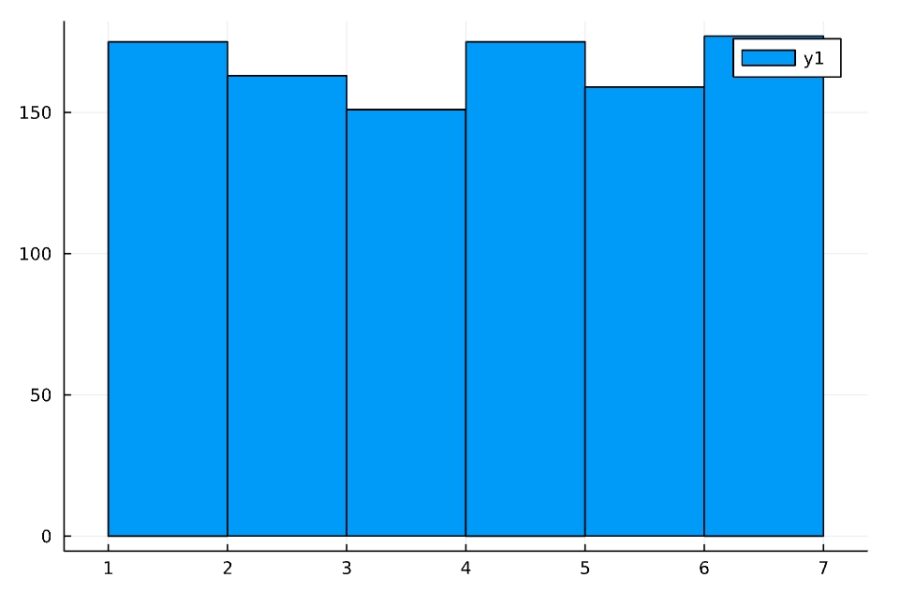
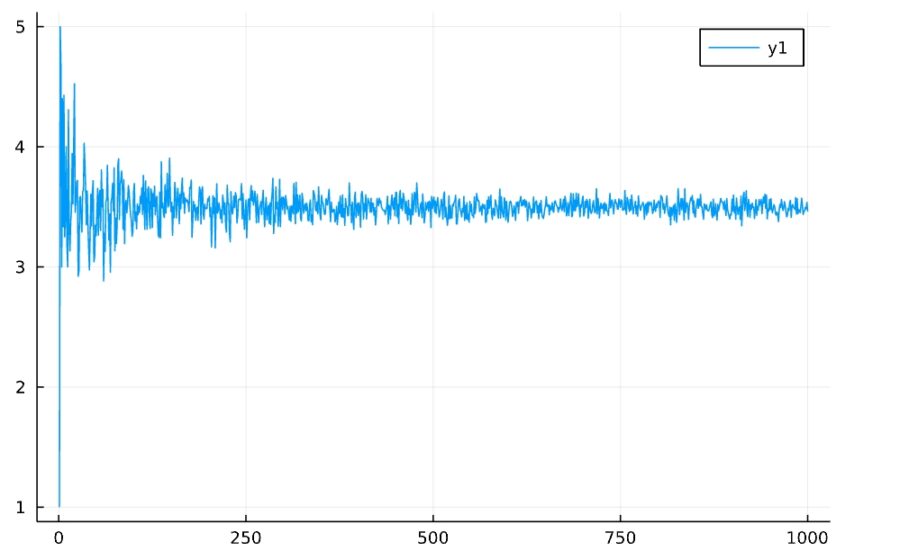
サンプルの平均がやがて理論的な平均(ここでは\(3.5\))に近づいていくという性質が、大数の法則です。
1 2 3 | Random.seed!(2022) f(n) = mean(rand(d1,n)) plot(1:1000,f) |
サンプル平均の正規化されたヒストグラムを作ってみましょう。その面積が起こりうる確率(相対頻度)を表すようになっています。
1 2 3 4 | Random.seed!(2022) f(n) = mean(rand(d1,n)) x = [f(i) for i in 1:1000] histogram(x, normalize=true) |
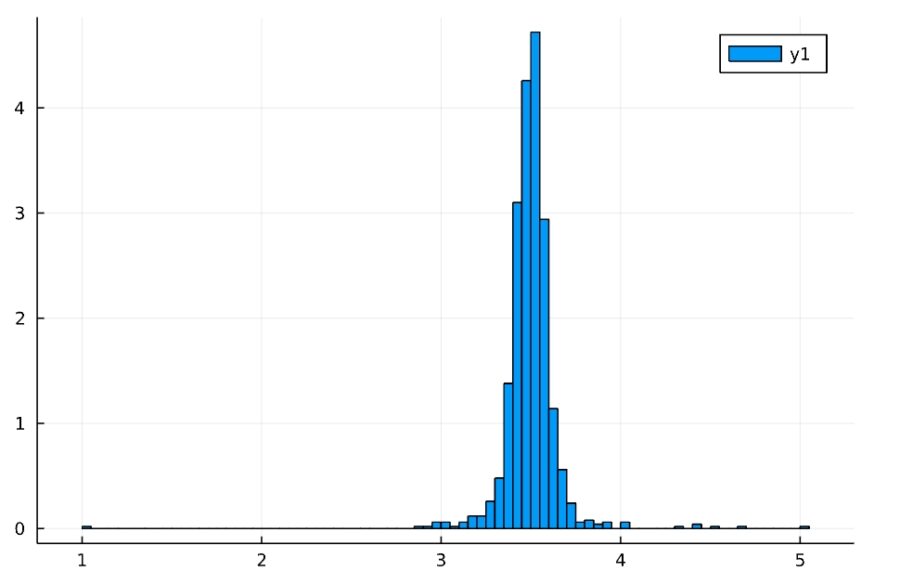
中心極限定理によると、\(M_n \sim \mathrm{Normal}(\mu , \frac{\sigma^2}{n}) \)と近似できます。
「pdf(分布,x)」で分布の確率密度関数が作れます。
1 2 3 | n_pdf(x) = pdf(Normal(mean(d1), var(d1)/1000),x) histogram(x, normalize=true) plot!(n_pdf, xlims=[1,5]) |

確率密度関数の比較だと、少しわかりにくいですが、確かに近似できていそうですね。
標準化を施した平均誤差のヒストグラムを描いてみましょう。
1 2 3 4 5 6 | Random.seed!(2022) g(n) = sqrt(n)*(mean(rand(d1,n))-mean(d1)) / std(d1) x = [g(i) for i in 1:1000] n2(x) = pdf(Normal(0, 1),x) histogram(x,normalize=true) plot!(n2) |
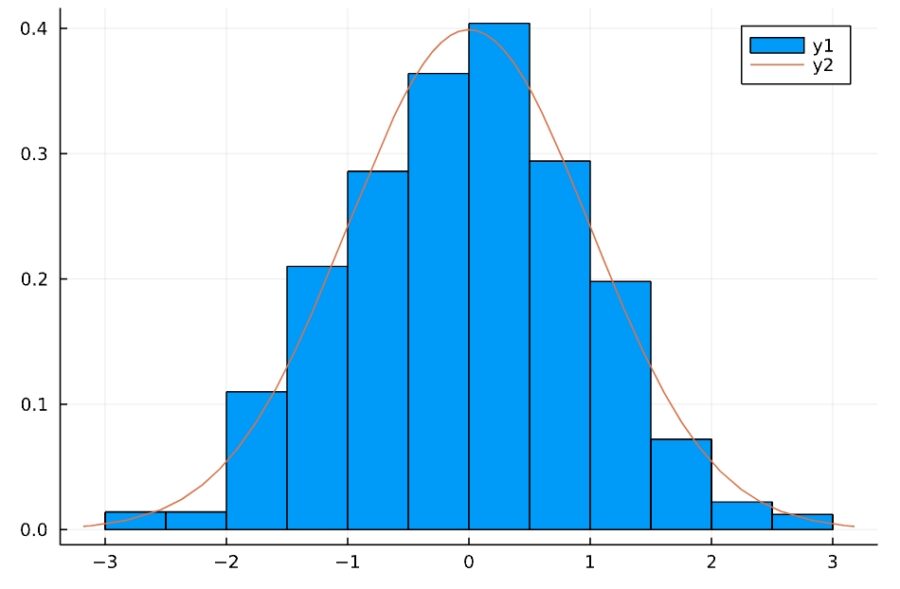
誤差が標準正規分布に従っているのが、よくわかりますね。
累積分布関数の観点から、比較してみましょう。
サンプル\(x\)の累積分布関数\(F(y)=P(Z_n \leq y)\)は
1 2 3 4 | function sample_cdf(x,y) a = length([b for b in x if b<= y])/length(x) return sum(a) end |
と定義できます。そのグラフを描いてみると、
1 2 3 | h(y) = sample_cdf(x,y) y = -5:0.1:5 plot(h) |

標準正規分布の分布関数と比較すると、よく近似していることがわかりますね。
1 2 3 4 | d = Normal(0,1) Φ(z) = cdf(d,z) plot(h) plot!(Φ) |
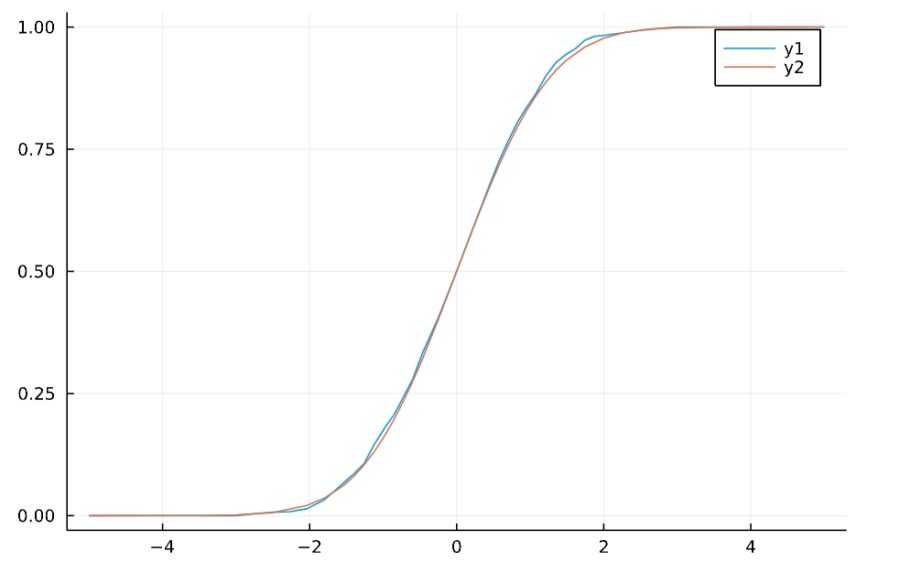
(サンプルに関する累積分布関数は、一般に経験的累積分布関数 eCDF と呼ばれています。StatsBase.jlでは、ecdfという関数が用意されていますね。)
これはサンプルの平均や和に関する確率が、(標準)正規分布の累積分布関数によって近似して計算できることを意味します。
例えば、1000回サイコロを振って、出る目の平均が\(3.4\)以下となる確率を求めたいとしましょう。
\[\begin{aligned} P(M_n \leq 3.4) &=P(\frac{M_n-\mu}{ \frac{\sigma}{\sqrt{n}}} \leq \frac{3.4- \mu}{\frac{\sigma}{\sqrt{n}}})\\ &\sim \Phi(\frac{3.4- \mu}{\frac{\sigma}{\sqrt{n}}}) \end{aligned}\]
なので、これを計算すると
1 | Φ(sqrt(1000)*(3.4-mean(d1))/std(d1)) |
1 | 0.03203875322552964 |
約\(3\%\)であることがわかります。これはめったにないことで、多くの場合は1000回サイコロを振れば平均は\(3.4\)以上になるということです。
大数の法則は、サンプルから平均のピンポイントの値を推定すること、点推定に役立ちます。これに対し中心極限定理は、サンプルから平均とどれだけずれる可能性があるかを区間に応じて推定すること、区間推定に役立ちます。
二項分布
中心極限定理の強力なところは、母集団の分布によらず、さまざまな分布に関して成り立つことです。
正規化された平均誤差のヒストグラム、確率分布関数をいくつか描いてみましょう。
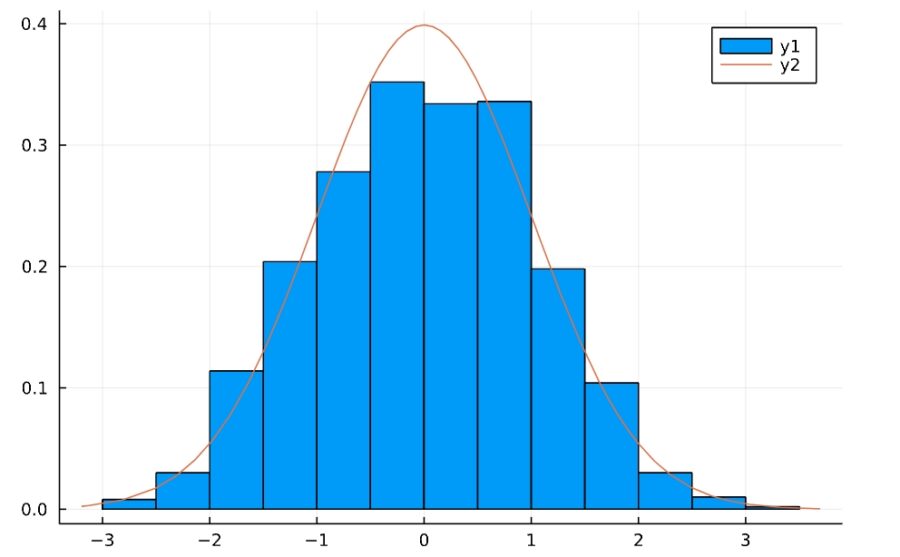
「Binomial(n,p)」が試行回数\(n\)、成功確率\(p\)の二項分布です。
1 2 3 4 5 6 7 | d2 = Binomial(30,0.8) Random.seed!(2022) g(n) = sqrt(n)*(mean(rand(d2,n))-mean(d2)) / std(d2) x = [g(i) for i in 1:1000] histogram(x,normalize=true) plot!(n2) |
1 2 3 4 | h(y) = sample_cdf(x,y) y = -5:0.1:5 plot(h) plot!(Φ) |
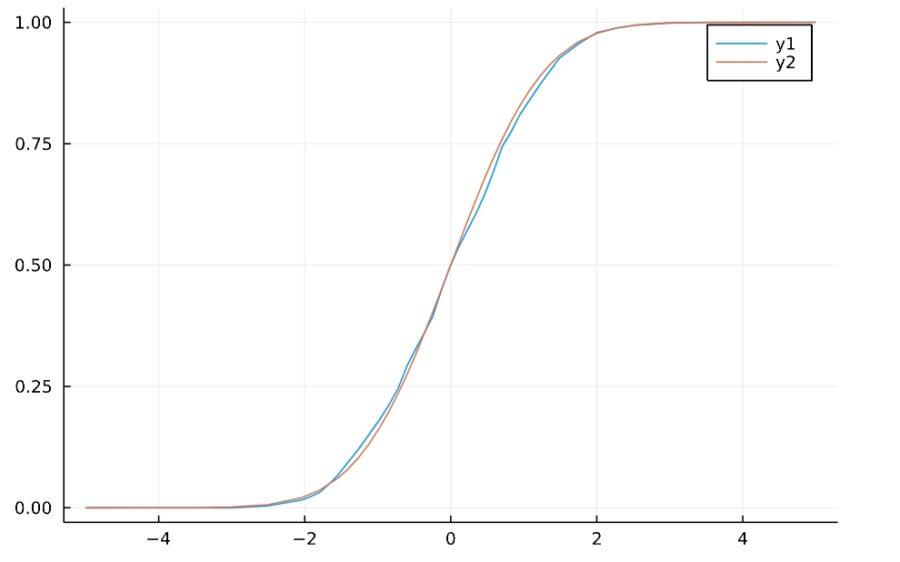
ポアソン分布
Poisson(λ)が発生頻度\(\lambda\)のポアソン分布です。
1 2 3 4 5 6 7 | d3 = Poisson(3) Random.seed!(2022) g(n) = sqrt(n)*(mean(rand(d3,n))-mean(d3)) / std(d3) x = [g(i) for i in 1:1000] histogram(x,normalize=true) plot!(n2) |
1 2 3 4 | h(y) = sample_cdf(x,y) y = -5:0.1:5 plot(h) plot!(Φ) |
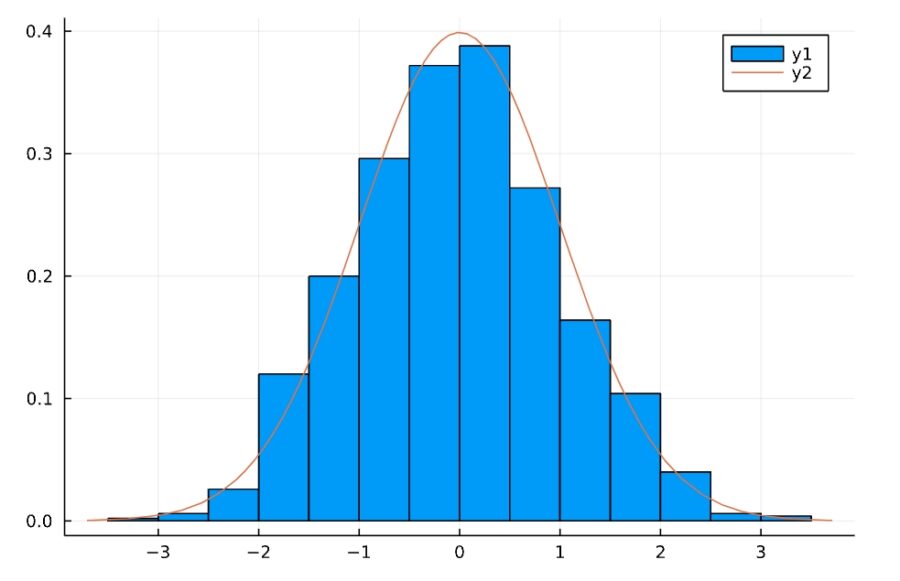

正規分布
もちろん、正規分布から取り出したサンプルについても中心極限定理は成り立ちます。
Normal(μ,σ)が平均\(\mu\)、標準偏差\(\sigma \)の正規分布です。
1 2 3 4 5 6 7 | d4 = Normal(50,10) Random.seed!(2022) g(n) = sqrt(n)*(mean(rand(d4,n))-mean(d4)) / std(d4) x = [g(i) for i in 1:1000] histogram(x,normalize=true) plot!(n2) |
1 2 3 4 | h(y) = sample_cdf(x,y) y = -5:0.1:5 plot(h) plot!(Φ) |
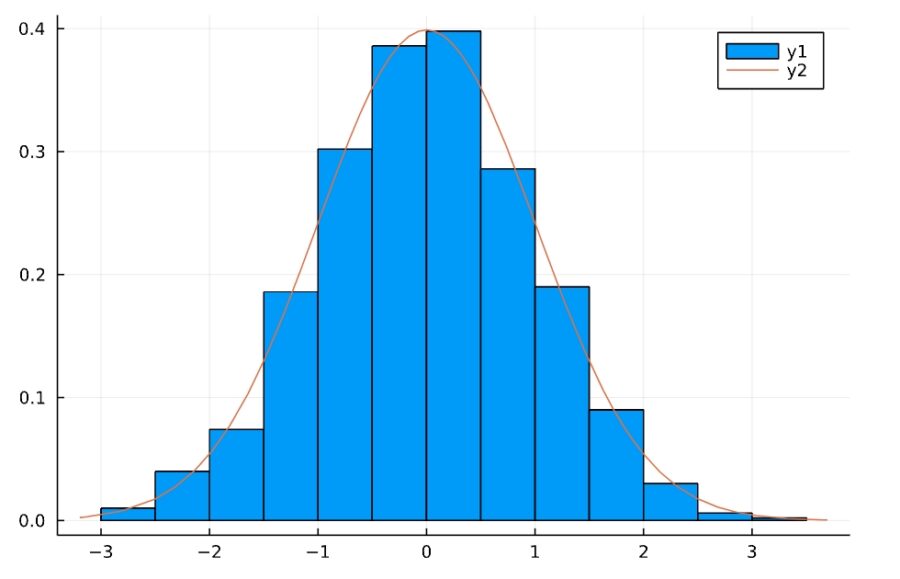

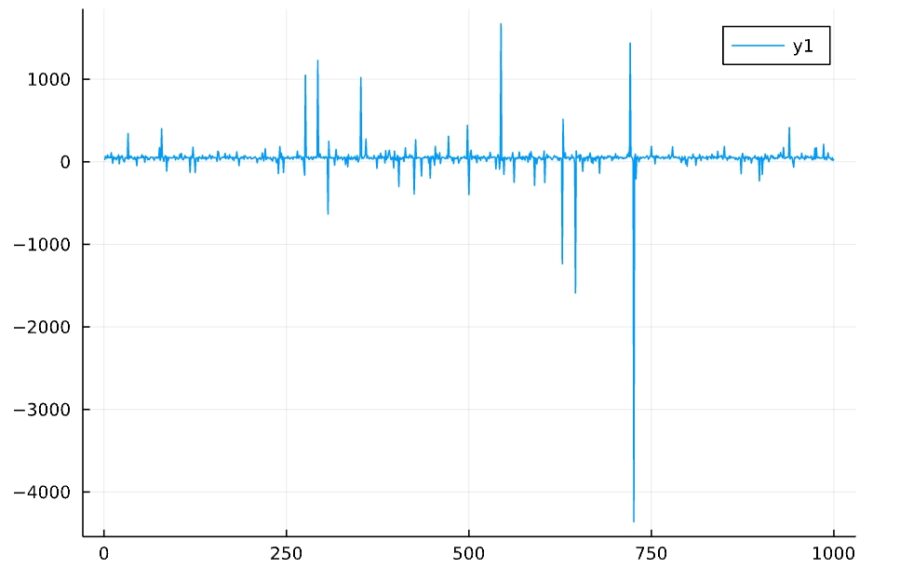
コーシー分布
中心極限定理の適用範囲は広いですが、限定もあります。平均と分散は有限値として存在しなければならないのです。
コーシー分布は、平均と分散が存在しない(発散する)例です。したがって、平均誤差の式
\[Z_n = \frac{M_n -\mu}{\frac{\sigma}{\sqrt{n}}}\]
は意味をなさず、中心極限定理は成り立ちません。
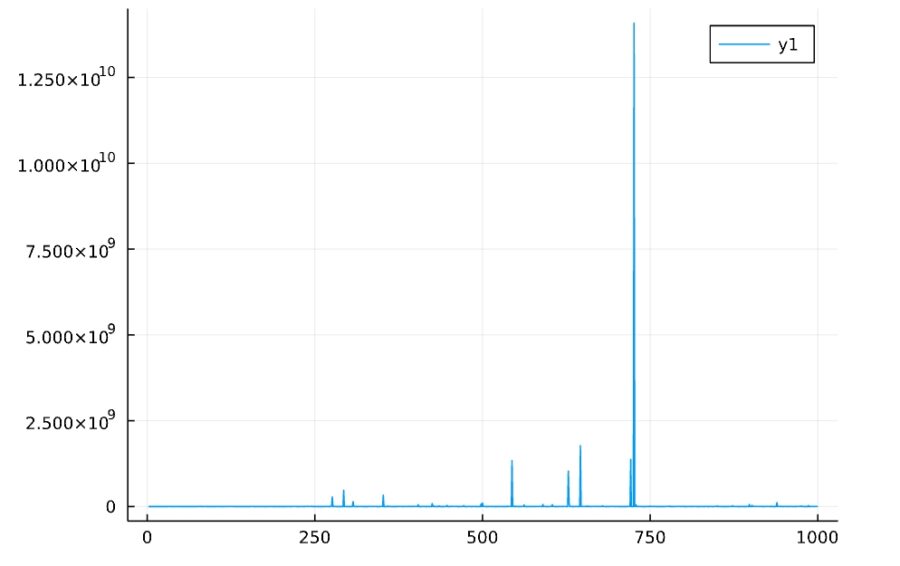
サンプルの平均や分散を計算してみても、一定の値には近づかないことがわかります。
1 2 3 4 5 | d5 = Cauchy(50, 10) Random.seed!(2022) f(n) = mean(rand(d5,n)) plot(1:1000,f) |
1 2 3 | Random.seed!(2022) f(n) = var(rand(d5,n)) plot(1:1000,f) |
以上、中心極限定理とは何か、Juliaでの計算例、その意味を紹介してきました。
中心極限定理の証明は熊谷「確率論」などを参照してください。
まずはコンピュータで数値計算をして確かめたり、確率を正規分布で近似計算してみると、その意味や応用が理解しやすいでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)
共立出版 (2003-03-15T00:00:01Z)
¥2,065 (中古品)
こちらもおすすめ
離散確率分布とは:一様分布、ベルヌーイ分布、二項分布、ポアソン分布を例に