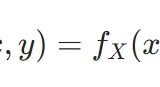どうも、木村(@kimu3_slime)です。
今回は、2次元の正規分布、分散共分散行列とは何か、具体例をもとにもとに紹介します。
2次元の正規分布、分散共分散行列とは
一般形の定義
2次元の正規分布は、1次元の正規分布を2次元の確率分布として一般化したものです。
2つのデータに関する関係、例えば国語と算数のテストの点数、人間の身長と体重などを分析するときに使えます。
\(x \in \mathbb{R}^2\)として、同時確率密度関数を
\[f(x) = \frac{1}{2\pi \sqrt{\det \Sigma}} \exp (-\frac{1}{2} (x-\mu)^\top \Sigma ^{-1} (x-\mu))\]
とする確率分布\(\mathrm{MvNormal}(\mu, \Sigma)\)を、2次元の正規分布(two-dimensional normal distribution)と呼びます。2次元に限らず一般の次元でも考えることができ、多変量正規分布(multivariate normal distribution)と呼ばれるものです。正規分布はガウス分布とも呼ばれます。
パラメータ\(\mu, \Sigma\)の説明をしましょう。
1変数の正規分布は
\[f(x) = \frac{1}{ \sqrt{2\pi \sigma}} \exp (-\frac{1}{2} \frac{(x-\mu)^2}{\sigma})\]
という形でした。\(\mu\)が平均、\(\sigma ^2\)が分散(\(\sigma\)が標準偏差)に対応するパラメータです。
2次元の正規分布では、平均は\(\mu = (\mu_X, \mu _Y)\)と2次元のベクトルになっています(平均ベクトル mean vector)。\(\mu _X =E(X), \mu _Y = E(Y)\)と書くことも。
指数関数の中身の2次関数\(\frac{(x-\mu)^2}{\sigma}\)は、2次形式\((x-\mu)^\top \Sigma ^{-1} (x-\mu)\)として一般化されました。
1次元の標準偏差\(\sigma\)に対応するのが、2次元の正方行列\(\Sigma\)です。その中身は
\[\Sigma = \begin{pmatrix} V(X)& \mathrm{Cov}(X,Y) \\ \mathrm{Cov}(Y,X) & V(Y) \end{pmatrix}\]
です。\(V\)は分散、\(\mathrm{Cov}\)は共分散を意味します。それぞれ\(\sigma _X , \sigma _Y\)、\(s_{XY}, s _{YX}\)と書くことも。
この行列を分散共分散行列(variance-covariance matrix)、または単に共分散行列(covariance matrix)と呼びます。
分散と共分散には\(V(X) = \mathrm{Cov}(X,X)\)という関係があること、共分散のパラメータは実質1つ\(\mathrm{Cov }(X,Y)= \mathrm{Cov}(Y,X)\)であることに注意しましょう。共分散の性質から、共分散行列は対称な正定値行列でなければなりません。
平均を2次元にすると、xに関する平均、yに関する平均が出てくるのはわかりやすいです。一方、分散を2次元にすると、xに関する分散、yに関する分散だけでなく、xとyの関係性ーー共分散を考える必要があります。
百聞は一見にしかずということで、具体的な平均ベクトルや共分共分散行列を与えて正規分布を見ていきましょう。
単位行列のとき
最も単純なケースは、共分散行列が単位行列\(I\)
\[\Sigma = \begin{pmatrix} 1&0\\0&1 \end{pmatrix}\]
のときです。平均ベクトルを\(\mu= (0,0)\)としましょう。
このとき、\(\det \Sigma =1 ,\Sigma ^{-1} =I\)です。したがって、確率密度関数は
\[\begin{aligned} f(x,y) &= \frac{1}{2\pi } \exp (-\frac{1}{2} (x ,y) \cdot \begin{pmatrix} x\\y \end{pmatrix}) \\ &= \frac{1}{2\pi} \exp(-\frac{1}{2}(x^2+y^2))\end{aligned}\]
です。かなりわかりやすくなりましたね。
平均\((0,0)\)、分散\((1,1)\)、共分散\(0\)のケースは、2次元の標準正規分布と呼ばれるものです。
グラフと等高線を図示すると次の通り。

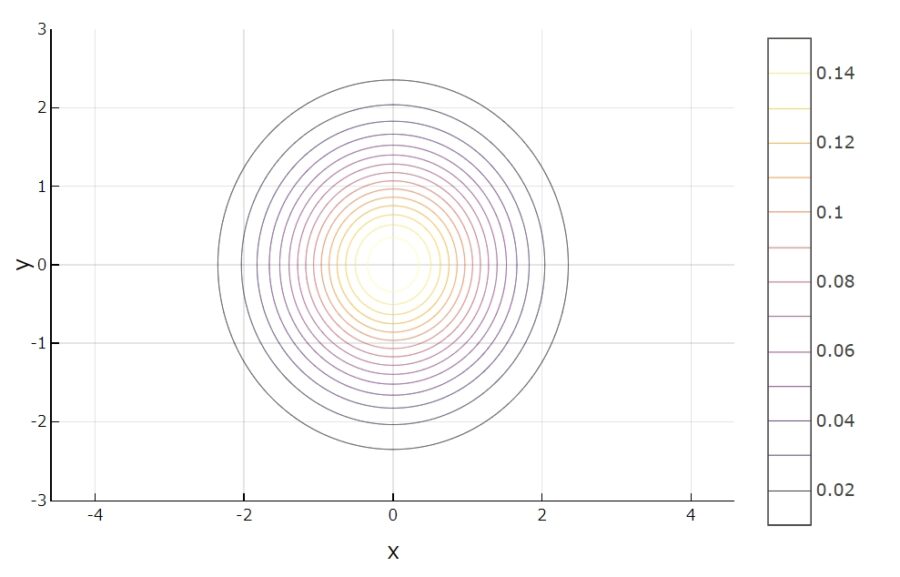
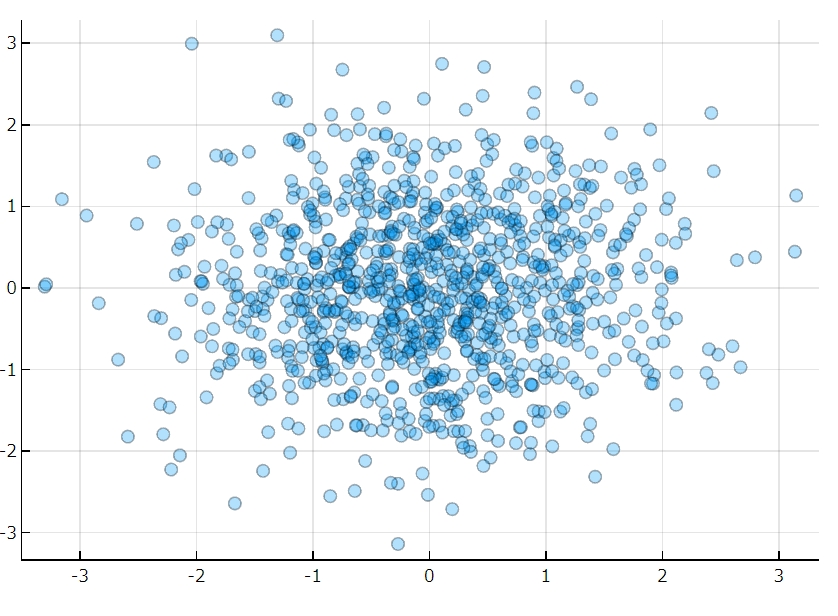
この分布に従うランダムなデータの散布図は次の通り。平均付近に集中しています。
対角行列のとき
続いて、平均ベクトルが\(\mu =(150,50)\)、共分散行列が
\[\Sigma = \begin{pmatrix} 50&0\\0&10 \end{pmatrix}\]
となるケースを考えましょう。
確率密度関数のグラフと等高線は次の通り。
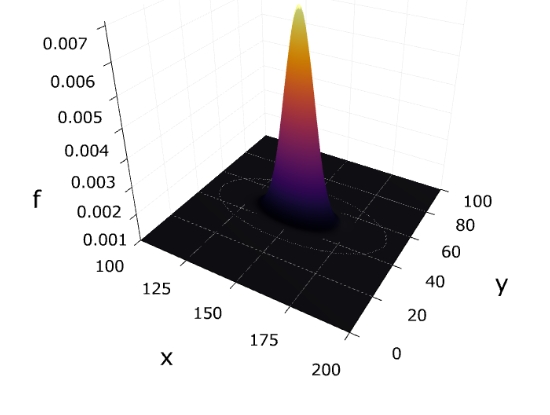
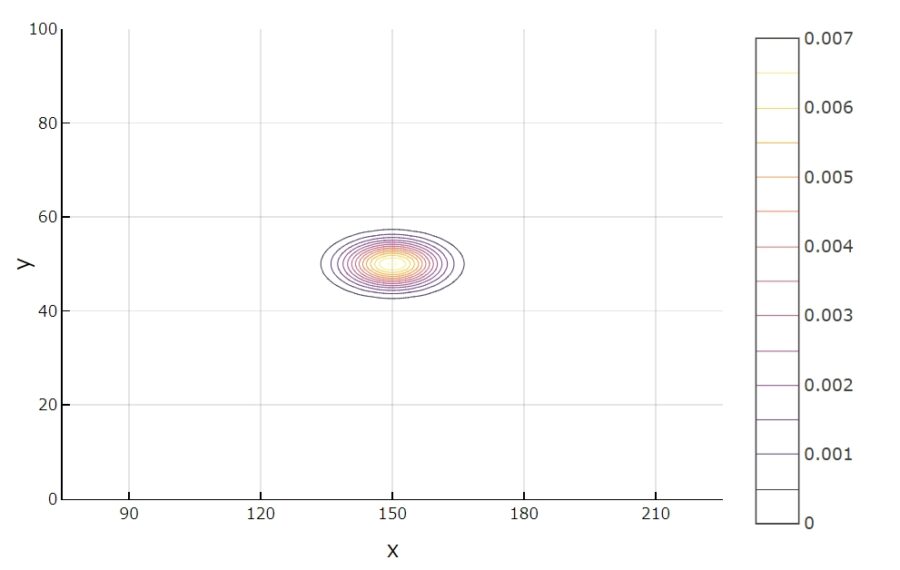
平均が確かに\((150,50)\)に移動していること、\(x\)方向の分散が大きく等高線が楕円になっていることが読み取れます。
この分布に従うランダムなデータの散布図は次の通り。

今までに考えてきた例では、\(x,y\)の間に関係性がない(共分散が0、つまり相関係数が0=無相関)ことがわかります。
参考:Juliaで散布図・相関図を描き、相関係数を求める方法
共分散が正のとき
平均ベクトルが\(\mu =(0,0)\)、共分散行列が
\[\Sigma = \begin{pmatrix} 5&2\\2&1 \end{pmatrix}\]
のケースを考えましょう。共分散が正となっています。
確率密度関数のグラフと等高線は次の通り。
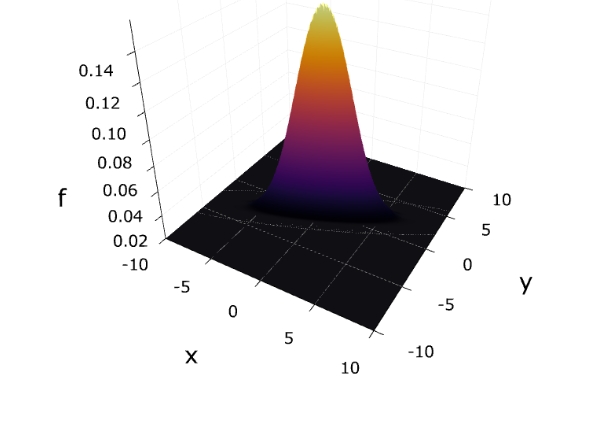
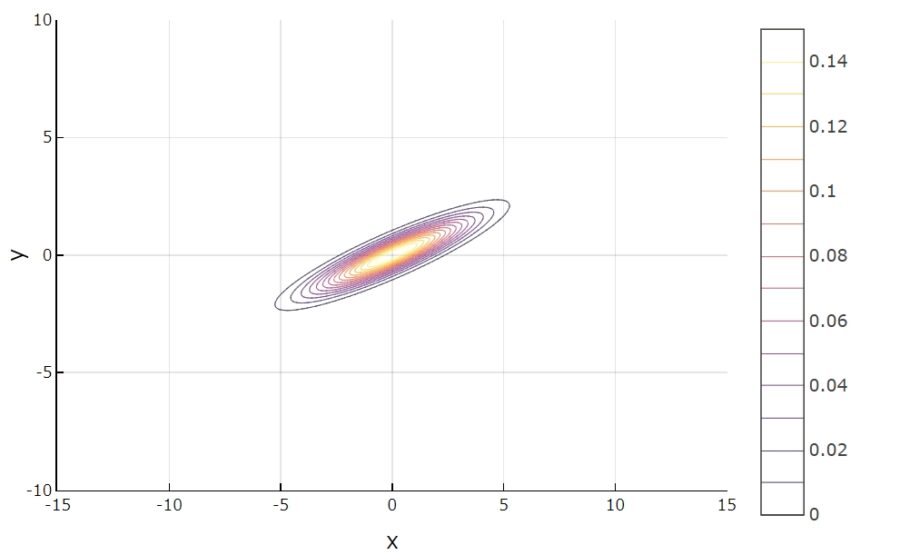
共分散が0のケースでは分散する方向が軸に沿っていましたが、今回はその方向が軸に沿っていません。
ちなみに、共分散行列の固有ベクトル(の近似値)\((0.4,0.9),(-0.9,0.4)\)は等高線の楕円の軸方向を表しています。
この分布に従うランダムなデータの散布図は次の通り。

\(x\)が増えるほど\(y\)が増えるという関係性、つまり正の相関があることが読み取れます。
この分布の相関係数は、約\(0.9\)です。
共分散が負のとき
同様に、平均ベクトルが\(\mu =(0,0)\)、共分散行列が
\[\Sigma = \begin{pmatrix} 6&-5\\-5&10 \end{pmatrix}\]
のケースを考えましょう。共分散が負となっています。
確率密度関数、等高線、ランダムなデータの散布図は次の通り。
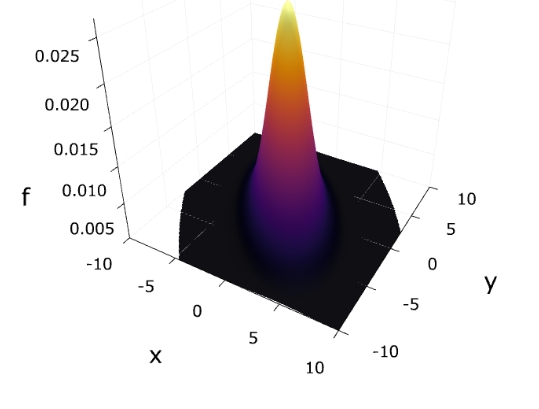
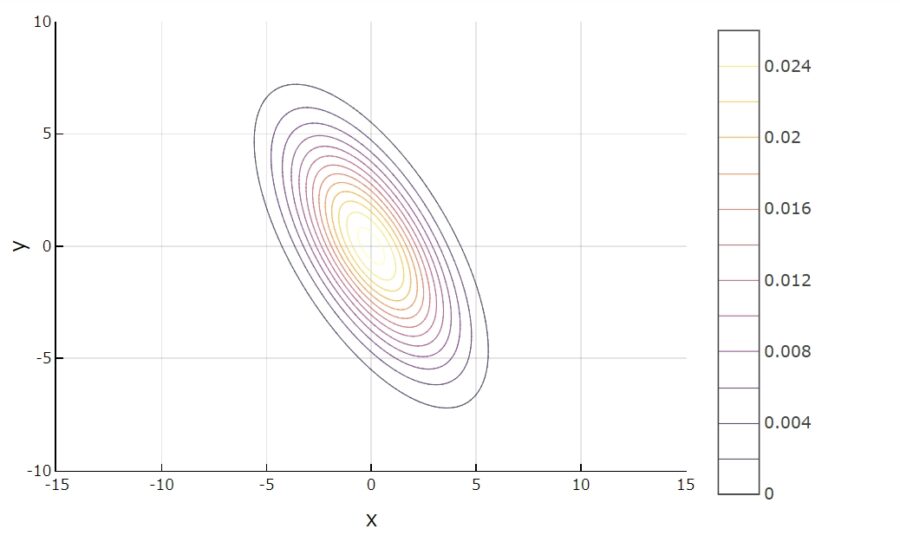
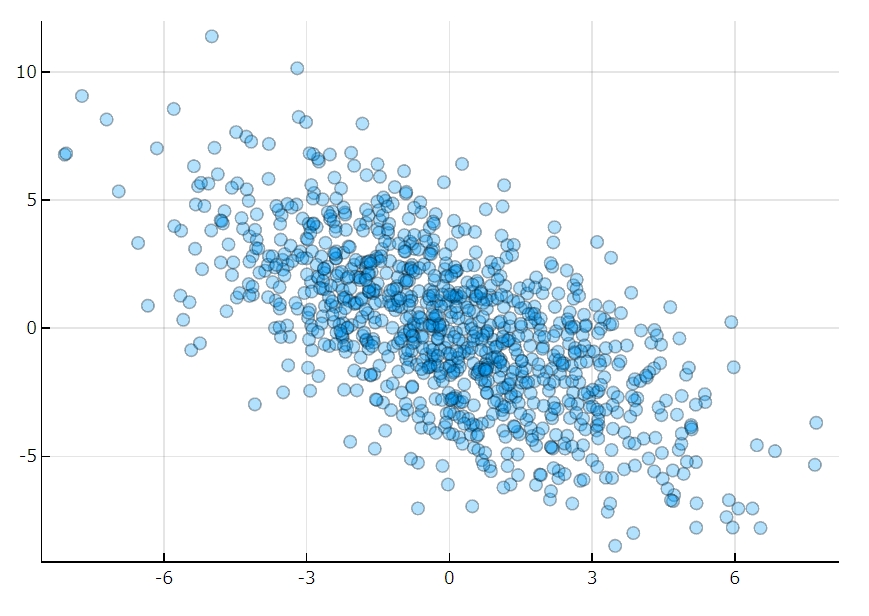
\(x\)が増えるほど\(y\)が減る、負の相関関係が表せていますね。
この分布の相関係数は、約\(-0.65\)です。
以上、2次元の正規分布、分散共分散行列とは何か、具体例をもとにもとに紹介してきました。
平均や分散、共分散を調整することで、無相関・正の相関・負の相関を持つ2つのデータの正規分布的な関係を表せて、便利なことがわかりますね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)