どうも、木村(@kimu3_slime)です。
今回は、2変数の連続同時確率分布、周辺分布とは何か、一様分布を例に紹介します。
2変数の離散確率分布とは
2次元の確率分布
\(1\mathrm{m^2}\)の平板の上に水滴を落とし、その中で落ちた位置について確率的に考えてみましょう。
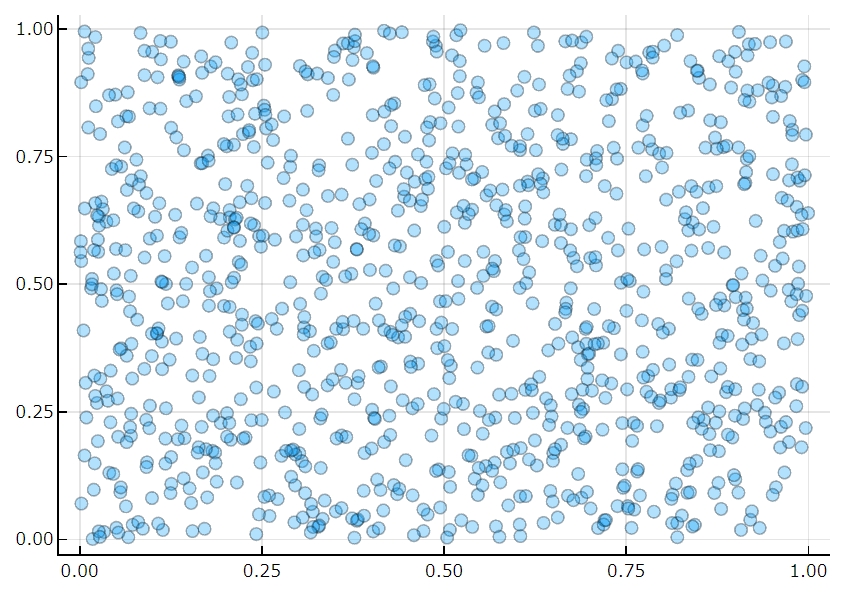
起こりうる結果、考える正方形は閉区間の直積集合\(\Omega =[0,1]\times [0,1]\)として表せます。
平板のどこにでも同じように(一様に)落ちると仮定するとき、\(A\subset \Omega\)に落ちる確率は
\[P(A) = \mu(A)\]
と表せます。ただし、\(\mu(A)\)は\(A\)の面積です。
例えば、\(A=[0,\frac{1}{2}]\times [0,\frac{1}{2}]\)に落ちる確率は、\(P(A)= \frac{1}{4}\)となります。
このような確率測度を、一般に2次元の確率分布(two-dimensional probability distribution)と呼びます。
連続確率変数、確率密度関数
水滴を落とす試行を、変数を分けて考えるために、2つの連続確率変数\(X,Y\)を考えましょう。\(Z(\omega)=(X(\omega), Y(\omega))\)という組により決まる確率変数\(Z:\Omega \to \mathbb{R}\)を、2次元の連続確率変数(two-dimensional continuous random variable)と呼びます。
1次元の確率変数で累積分布関数を考えたように、2次元でも同じことを考えましょう。
\[F_{X,Y}(x,y) = P(X\leq x,Y\leq y)\]
により定まる2変数関数\(F_{X,Y}\)を、確率変数\((X,Y)\)の(同時)累積分布関数(cdf; culminative distribution function)と呼びます。
また、累積分布関数を積分によって表せる関数、つまり
\[F_{X,Y}(x,y)= \int_{-\infty}^y \int_{-\infty}^x f_{X,Y}(s,t)dsdt\]
を満たす関数\(f_{X,Y}\)を、(同時)確率密度関数(pdf; probability density function)と呼びます。
逆に、複数の確率変数や確率密度関数に対応して決まる多次元の確率測度\(P\)を、同時確率分布(joint probability distribution)と呼びます。今回の例は、2つの確率変数、確率分布を結合したものです。
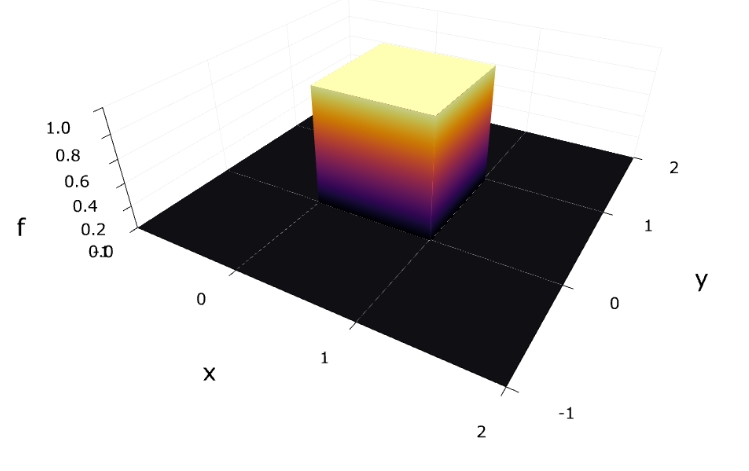
正方形平板に水滴を落とす試行において、具体的に考えてみましょう。確率密度関数は
\[f_{X,Y}(x,y)= \begin{cases} 1 & ((x,y) \in [0,1]\times[0,1])\\0 & (それ以外)\end{cases}\]
です。
すべての事象を考えたときの確率は1なので、確率密度関数の総和は
\[\int_{-\infty}^\infty \int_{-\infty}^\infty f_{X,Y}(s,t)dsdt=1\]
という性質を満たすように与えなければなりません。
実際上の例では、
\[\begin{aligned} &\int_{-\infty}^\infty \int_{-\infty}^\infty f_{X,Y}(s,t)dsdt\\ &= \int_0^1 \int_0^1 1 ds dt \\ &=1\end{aligned}\]
で、条件を満たしています。
一般に長方形\(R\)における一様分布を考えるなら、\(f(x,y) = \frac{1}{\mu(R)}\)とすれば良いですね。今回は\(\mu (R)=1\)に対応しています。
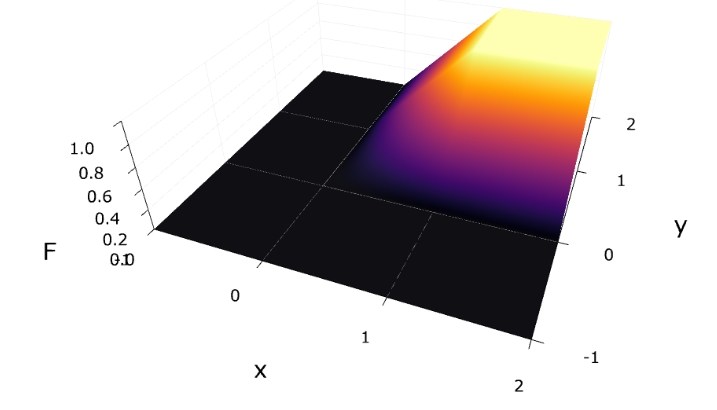
一様分布の例で累積分布関数を求めると、\((x,y)\in [0,1]\times[0,1]\)のとき
\[\begin{aligned} &F_{X,Y}(x,y)\\&= \int_{0}^y \int_{0}^x 1dsdt \\&=xy\end{aligned}\]
となります。\(x > 1\)かつ\(y \in [0,1]\)のときは
\[\begin{aligned} &F_{X,Y}(x,y)\\&= \int_{0}^y \int_{0}^1 1dsdt \\&=y\end{aligned}\]
で、\(x \in [0,1]\)かつ\(y >1\)のときは
\[\begin{aligned} &F_{X,Y}(x,y)\\&= \int_{0}^1 \int_{0}^x 1dsdt \\&=x\end{aligned}\]
、それ以外のときは\(0\)になります。これを図示すると次の通り。
周辺分布
2次元の確率分布について、一方の変数について条件を課さずに得る確率分布
\[P_X (A_1): = P(X \in A_1 ,Y \in \mathbb{R} )\]
\[P_Y (A_2): = P(X \in \mathbb{R} ,Y \in A_2 )\]
をそれぞれ\(X,Y\)の周辺分布(marginal distribution)と呼びます。
これに対応して、
\[\begin{aligned} f_{X}(x) &= \int_{-\infty}^\infty f_{X,Y}(x,y)dy\end{aligned}\]
\[\begin{aligned} f_{Y}(y) &= \int_{-\infty}^\infty f_{X,Y}(x,y)dx\end{aligned}\]
によって定まる1変数関数をそれぞれ\(X,Y\)の周辺確率質量関数(marginal probability mass function)と呼びます。
一様分布の例ならば、\(x,y \in [0,1]\)ならば
\[\begin{aligned} f_{X}(x) &= \int_0^1 1 dy \\&=1 \end{aligned}\]
\[\begin{aligned} f_{Y}(y) &= \int_0^1 1 dx \\&=1 \end{aligned}\]
で、それ以外なら\(0\)です。
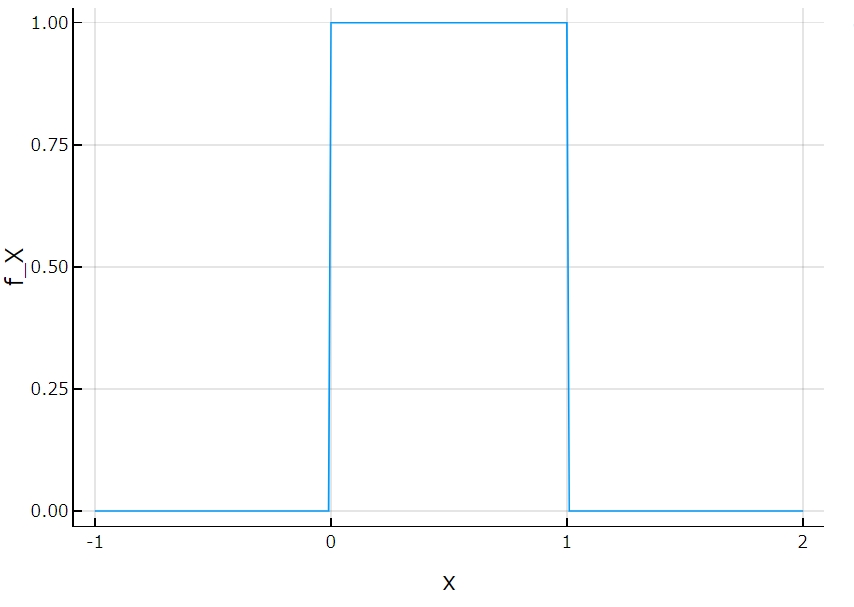
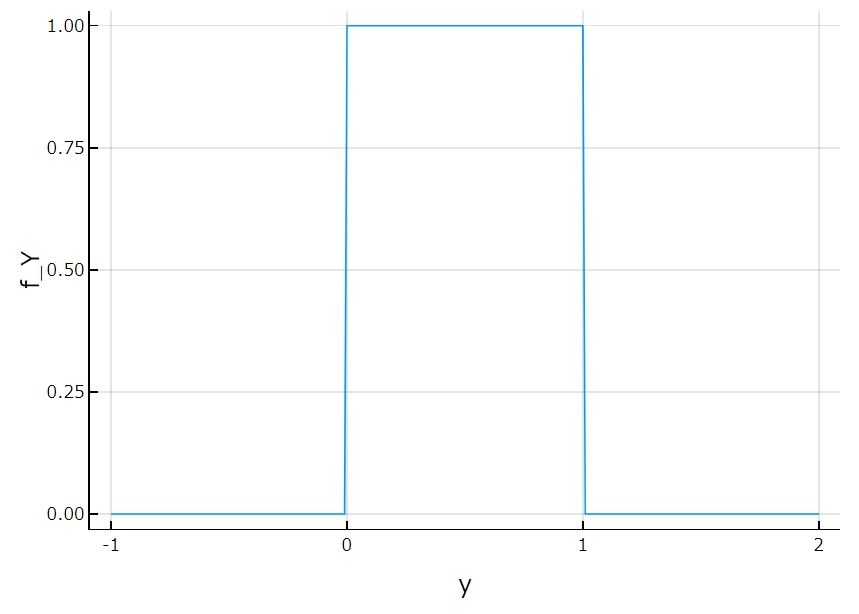
これはそれぞれの確率変数\(X,Y\)、一様分布の確率密度関数に対応していますね。
同様に、
\[\begin{aligned} F_{X}(x) &= P(X\leq x,Y\in \mathbb{R}) \\ &= \int_{-\infty} ^x f_{X}(s)ds\end{aligned}\]
\[\begin{aligned} F_{Y}(y) &= P(X\in \mathbb{R},Y\leq y) \\ &= \int_{-\infty} ^y f_{Y}(t)dt\end{aligned}\]
をそれぞれ\(X,Y\)の周辺確率質量関数(marginal probability mass function)と呼びます。
同時分布という用語では2つの変数をセットで考え、周辺分布という用語ではひとつの変数に注目し他方の結果を気にせずまとめている、という違いがありますね。
以上、2変数の連続同時確率分布、周辺分布とは何か、一様分布を例に紹介してきました。
他にもさまざまな連続同時確率分布を考えることはできますが、その最も簡単な例として一様分布を知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)