ベルヌーイ分布、二項分布の平均値、分散の求め方

どうも、木村（@kimu3_slime）です。

今回は、ベルヌーイ分布、二項分布の平均値、分散の求め方を紹介します。

ベルヌーイ分布の平均値、分散

平均値、分散の定義をおさらいしておきます。

確率分布\(P\)に従う離散確率変数を\(X\)、確率質量関数を\(f(x):=P(X=x)\)とします。確率変数の平均値、または期待値は

\[E(X):= \sum_{k} x_k f(x_k)\]

で、分散には

\[V(X) =\sum_{k} (x_k-E(X))^2 f(x_k)\\= E(X^2) – (E(X))^2\]

確率\(p\)（\(0 \leq p \leq 1\)）で一方の結果が起こるベルヌーイ分布Bernoulli(p)の確率質量関数は、

\[f(k)= \begin{cases}1-p & (k=0 )\\p & (k=1)\end{cases}\]

です。

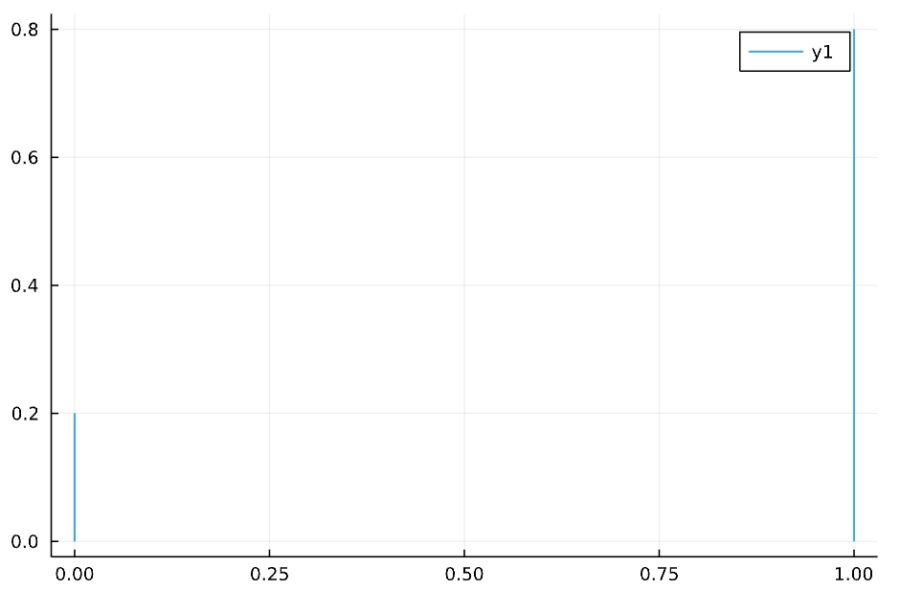
平均値を求めてみましょう。

\[\begin{aligned} E(X) &= 0\cdot(1-p)+1\cdot p \\&=p \end{aligned}\]

です。

\[\begin{aligned} E(X^2) &= 0^2\cdot(1-p)+1^2\cdot p \\&=p \end{aligned}\]

なので、分散は

\[\begin{aligned} V(X)&= E(X^2) -(E(X))^2 \\ &= p-p^2 \\ &= p(1-p)\end{aligned}\]

となります。これは2次関数であり、分散が最も大きくなるのは\(p=\frac{1}{2}\)のときですね。

例えば\(p=0.8\)のときは、平均値は\(0.8\)、分散は\(0.16\)です。

nを試行回数、pを一方が起こる確率とする二項分布Binomial(n,p)について、その確率質量関数は

\[f(k) =C(n,k) p^k (1-p)^{n-k}\]

です。ただし、\(C(n,k)\)は二項係数です。

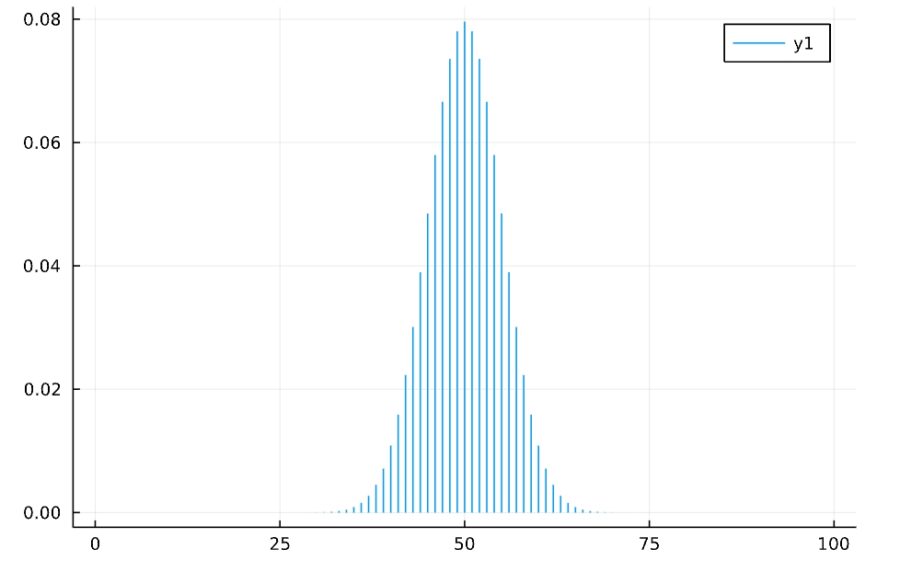
定義にしたがって平均値や分散を計算することもできますが、複雑で難しくなります。

今回はいくつかの一般的な結果を認めた上で、ベルヌーイ分布から二項分布の結果を導いてみましょう。

\(X_1,\dots,X_n\)をベルヌーイ分布に従う独立な確率変数とする。\(S_n = \sum_{k=1}^n X_k\)は二項分布に従う（二項分布とは、ベルヌーイ分布の繰り返しである）。
期待値の加法性：\(X,Y\)を確率変数とすると、\(E(X+Y)=E(X)+E(Y)\)
分散の加法性：\(X,Y\)を独立な確率変数とすると\(V(X+Y)=V(X)+V(Y)\)

証明は例えば熊谷「確率論」を参照。

確率変数\(X_k\)はすべてベルヌーイ分布に従うので、さきほどの結果から\(E(X_k)=p\)、\(V(X_k)=p(1-p)\)です。

期待値の加法性から、

\[\begin{aligned} E(S_n) &= \sum_{k=1}^n E(X_k) \\ &= np\end{aligned}\]

です。各試行の独立性に注意して、分散の加法性から、

\[\begin{aligned} V(S_n) &= \sum_{k=1}^n V(X_k) \\ &= np(1-p)\end{aligned}\]

と求められました。ベルヌーイ分布の平均値、分散に試行回数をそのままかけた形です。

例えば\(n=100, p = \frac{1}{2}\)ならば、平均値は\(50\)、分散は\(25\)となります。

以上、ベルヌーイ分布、二項分布の平均値、分散の求め方を紹介してきました。

ベルヌーイ分布の扱いは非常に簡単です。まずはそれを理解して、その組み合わせとしての二項分布を学ぶと良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。