どうも、木村(@kimu3_slime)です。
今回は、正規分布の1σ、2σ、3σ区間の確率の求め方、Juliaを利用した方法を紹介します。
正規分布の1σ、2σ、3σ区間の求め方
1σ、2σ、3σ区間とは
平均\(\mu\)、標準偏差\(\sigma\)の正規分布Normal(μ,σ)を考えましょう。それに従う確率変数\(X\)が、平均から1σ、2σ、3σの区間内の値を取る確率は、
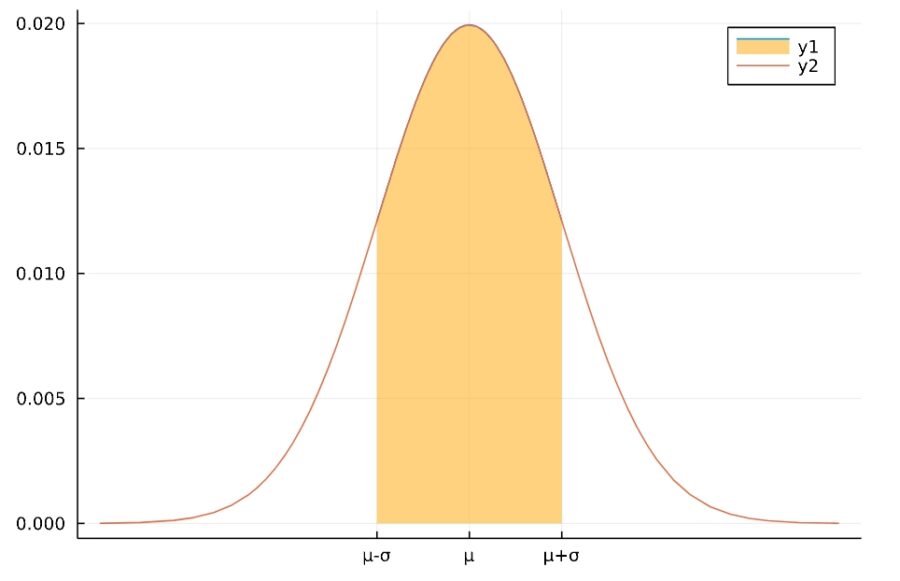
\[P(\mu-\sigma \leq X \leq \mu +\sigma) \simeq 68\%\]
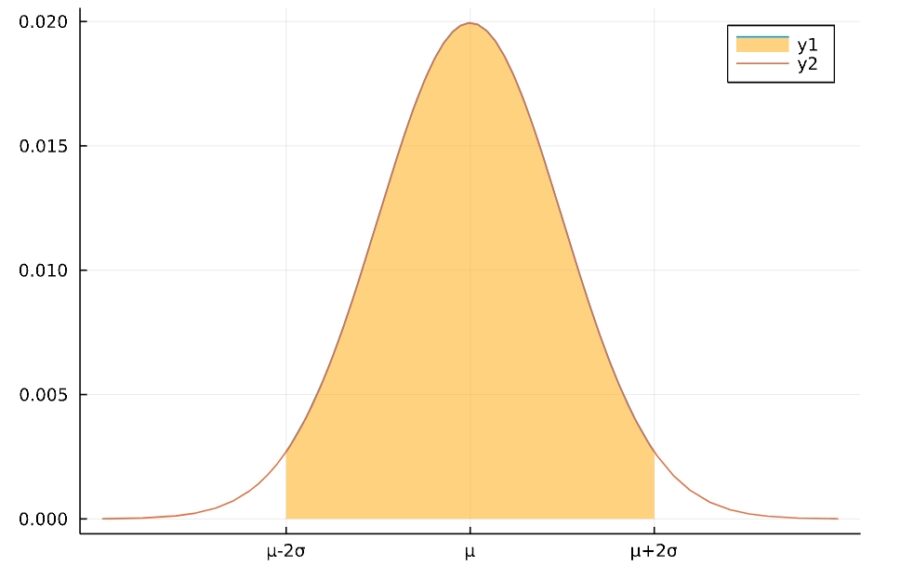
\[P(\mu-2\sigma \leq X \leq \mu +2\sigma) \simeq 95\%\]
\[P(\mu-3\sigma \leq X \leq \mu +3\sigma) \simeq 99.7\%\]
となります。これは68–95–99.7則(68–95–99.7 rule)と呼ばれる性質です。
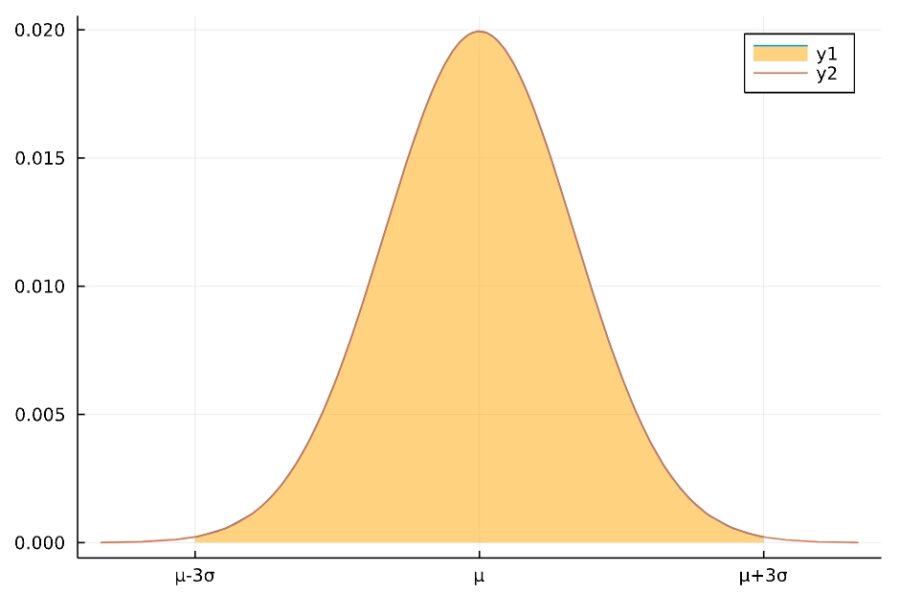
区間の確率と累積分布関数
この法則が正しいかどうか、調べてみましょう。
まず、正規分布に限らない一般的な連続確率分布\(P\)、 確率変数\(X\)、累積分布関数\(F\)について、
\[P(X \leq x) = F(x)\]
という関係があります(累積分布関数の定義)。これを使って、区間\([a,b]\)の確率、\(a\leq X \leq b\)となる確率を求めましょう。
\(a\leq X \leq b\)という集合は、\( X \leq b\)から\( X <a\)という集合を引いたもの(差集合\((X \leq b) \setminus(X <a)\))です。確率は共通部分がないときはバラバラに計算できるので(確率測度の加法性)、
\[\begin{aligned} P(a \leq X \leq b) &= P((X \leq b) \setminus(X <a)) \\ &=P(X \leq b) – P(X <a)\\ &= F(b)-F(a)\end{aligned}\]
となります。
標準正規分布への変換
これで正規分布に関する確率も計算できるわけですが、できれば平均、標準偏差によらない計算を実行したいです。
正規分布Normal(μ,σ)の累積分布関数を\(F\)、標準正規分布Normal(0,1)の累積分布関数を\(\Phi\)とすると、
\[F(x) = \int_{-\infty}^x \frac{1}{\sqrt{2\pi \sigma ^2} } \exp(-\frac{(s-\mu)^2}{2 \sigma^2})ds \]
\[\Phi(z) = \int _{-\infty} ^z \frac{1}{\sqrt{2\pi } } \exp(-\frac{t^2}{2 }) dt\]
です。ここで\(z= \frac{x-\mu}{\sigma}\)という変換をすると、\(F(x) = \Phi (\frac{x-\mu}{\sigma})\)という対応関係にあります。
なぜか。\(\Phi\)の式において、\(t = \frac{s -\mu}{\sigma}\)と変数変換しましょう。\(s= \sigma t +\mu\)です。積分区間\(t: -\infty \to \frac{x-\mu}{\sigma}\)は、\(s: -\infty \to x\)に対応します。変換倍率は\(\frac{dt}{ds}= \frac{1}{\sigma}\)です。したがって、
\[\begin{aligned} &\int _{-\infty} ^{\frac{x-\mu}{\sigma}} \frac{1}{\sqrt{2\pi } } \exp(-\frac{(t-\mu)^2}{2 }) dt \\ &= \int_{-\infty}^x \frac{1}{\sqrt{2\pi } } \exp(-\frac{(s-\mu)^2}{2 \sigma^2}) \frac{1}{\sigma}ds\end{aligned}\]
となり、一致することがわかりました。
正規分布のσ区間の確率
ここまでの結果をまとめれば、
\[\begin{aligned} &P(a \leq X \leq b) \\&= F(b)-F(a) \\ &= \Phi(\frac{b-\mu}{\sigma}) – \Phi(\frac{a-\mu}{\sigma})\end{aligned}\]
です。\(k\)を正の実数として、\(k\sigma\)区間\(\mu – k\sigma \leq X \leq \mu + k\sigma\)の確率は、
\[\begin{aligned} &P(\mu – k\sigma \leq X \leq \mu + k\sigma) \\ &= \Phi(k) – \Phi(-k)\end{aligned}\]
となりました。この値は、何σの区間を考えるかのみに依存し、\(\mu, \sigma\)に依存しませんね。
Juliaによる計算
では、正規分布のσ区間の確率を、Juliaで具体的に数値的に計算してみましょう。
StatsPlots, Distributionsを使うので、持っていなければインストールしておきましょう。
1 2 3 | using Pkg Pkg.add("StatsPlots") Pkg.add("Distributions") |
準備として、以下のコードを実行しておきます。
1 | using StatsPlots, Distributions |
「cdf(確率分布, 変数の値)」で累積分布関数が計算できます。
1 | cdf(Normal(0,1),1) |
1 | 0.841344746068543 |
さきほど求めたσ区間の確率の式を使えば、
1 2 3 4 | interval_probability(k) = cdf(Normal(0,1),k) - cdf(Normal(0,1),-k) interval_probability(1) interval_probability(2) interval_probability(3) |
1 2 3 | 0.6826894921370861 0.9544997361036416 0.9973002039367398 |
と1σ区間、2σ区間、3σ区間の確率を詳細に求めることができました。
信頼区間の理論では、その確率が95%、99%、99.9%となるようなkを使います。
1 | plot(interval_probability, xlims=[1.9,3.3]) |
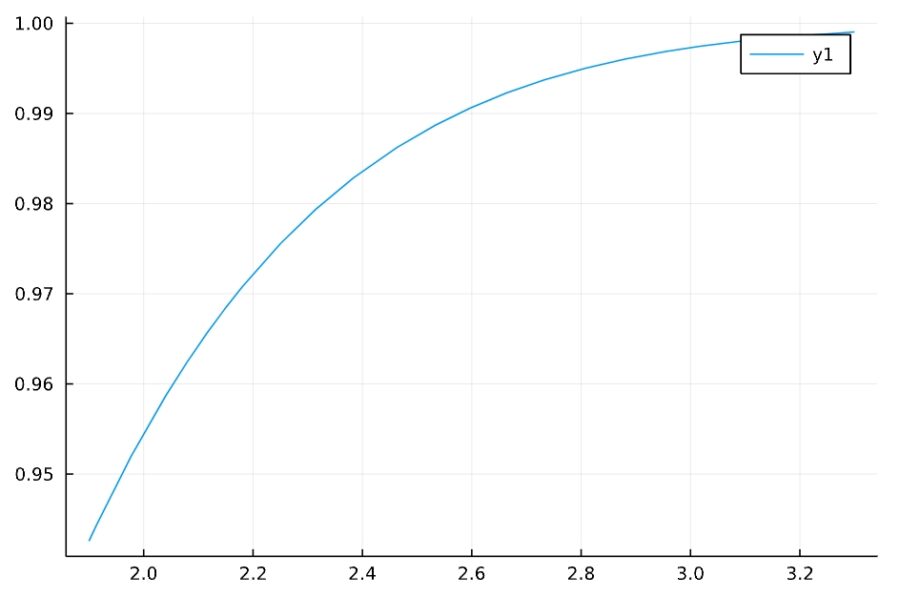
グラフを見ると、およその値に検討がつきますね。
95%、99%、99.9%区間の具体的な近似値としては、\(1.96, 2.58, 3.29\)が知られています。計算してみると、
1 2 3 | interval_probability(1.96) interval_probability(2.58) interval_probability(3.29) |
1 2 3 | 0.950004209703559 0.9901199684844588 0.9989981261724286 |
と精度の良い近似であることがわかりました。
以上、正規分布の1σ、2σ、3σ区間の確率の求め方、Juliaを利用した方法を紹介してきました。
教科書などに書かれている標準正規分布表を見て計算することもできますが、コンピュータを使うとより簡単でしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)