どうも、木村(@kimu3_slime)です。
今回は、Julia(SymPy)でスカラー場・ベクトル場の線積分を計算する方法を紹介します。
準備
SymPyを使うので、持っていなければインストールしておきましょう。
1 2 | using Pkg Pkg.add("SymPy") |
準備として、以下のコードを実行しておきます。
1 | using SymPy |
スカラー場の線積分
まず、今回の計算に変数として使う記号を用意しておきます。
1 | @vars x y z r θ t real=true |
SymPyにはline_integrateという関数がありますが、ベクトル場のケースに対応していないようなので、通常の積分方法(integrate)を使って、線積分を計算してみましょう。
スカラー場(実数値関数)\(f\)の曲線\(c(t)\)における線積分は
\[ \begin{aligned}\int _c f :=\int_a ^b f(c(t)) \| c^{\prime }(t)\| dt\end{aligned} \]
と定義されています。
まず、曲線の微分\(c^{\prime}(t)\)を計算するために、ベクトル値関数の微分を定義します。
1 2 3 | function diff_vec(c,t) return [diff(c[1],t) , diff(c[2],t)] end |
例えば、次のような結果が得られます。
1 2 3 | c = [t,t^2] diff_vec(c,t) (diff_vec(c,t)).norm() |
\[ \begin{aligned}\left[ \begin{array}{r}t\\t^{2}\end{array} \right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}1\\2 t\end{array} \right]\end{aligned} \]
\[ \begin{aligned}\sqrt{4 t^{2} + 1}\end{aligned} \]
スカラー場の曲線上での値(合成関数)を計算するには、「数式.subs(代入する変数、値)」で代入すれば良いです。
1 | (x+y).subs([(x,c[1]),(y,c[2])]) |
\[ \begin{aligned}t^{2} + t\end{aligned} \]
以上のことをまとめて、線積分を関数として定義しましょう。「integrate(関数,積分範囲)」で積分計算です。
1 2 3 4 5 | function lineint(f::Sym,c,a,b) return (integrate(f.subs([(x,c[1]),(y,c[2])]) * (diff_vec(c,t)).norm() , (t,a,b)) ) end |
関数の変数を「f::Sym」としているのは、インプットがSym(スカラー場)であるときのみ、この計算を行うというものです。
次のような経路に沿って、関数の線積分を計算してみましょう。
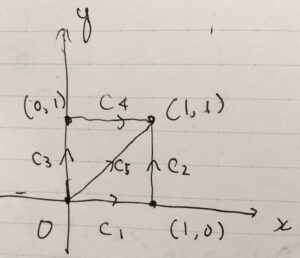
1 2 3 4 5 6 | c1 = [t,0] c2 = [1,t] c3 = [0,t] c4 = [t,1] c5 = [t,t] f1 = 2*x - 3*y |
\[ \begin{aligned}\left[ \begin{array}{r}t\\0\end{array} \right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}1\\t\end{array} \right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}0\\t\end{array} \right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}t\\1\end{array} \right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}t\\t\end{array} \right]\end{aligned} \]
\[ \begin{aligned}2 x – 3 y\end{aligned} \]
各経路での線積分は、次の通り。
1 2 3 4 | clist = [c1,c2,c3,c4,c5] for i in 1:5 display(lineint(f1,clist[i],0,1)) end |
\[ \begin{aligned}1\end{aligned} \]
\[ \begin{aligned}\frac{1}{2}\end{aligned} \]
\[ \begin{aligned}- \frac{3}{2}\end{aligned} \]
\[ \begin{aligned}-2\end{aligned} \]
\[ \begin{aligned}- \frac{\sqrt{2}}{2}\end{aligned} \]
ベクトル場の線積分
ベクトル場の線積分は
\[ \begin{aligned}\int _c f :=\int_a ^b \langle F(c(t)) ,c^{\prime }(t) \rangle dt\end{aligned} \]
と定義されます。これを関数として定義してみましょう。
ベクトル場\(F(x,y)\)の曲線上の値は、次のようにすれば良いです。
1 | ([x,y].subs([(x,c[1]),(y,c[2])])) |
\[ \begin{aligned}\left[ \begin{array}{r}t\\t^{2}\end{array}\right]\end{aligned} \]
ベクトルの内積は「a.dot(b)」です。
1 | ([x,y].subs([(x,c[1]),(y,c[2])])). dot( diff_vec(c,t) ) |
\[ \begin{aligned}2 t^{3} + t\end{aligned} \]
したがって、ベクトル場の線積分は、一般的には次のようにして計算できます。
1 2 3 4 5 | function lineint(F::Vector{Sym},c,a,b) return (integrate((F.subs([(x,c[1]),(y,c[2])])). dot( diff_vec(c,t) ) , (t,a,b)) ) end |
引数の型を「F::Vector{Sym}」と指定していて、インプットがベクトル場のときにこの計算が実行されます。
1 | methods(lineint) |
1 2 3 4 | # 2 methods for generic function lineint: lineint(f::Sym, c, a, b) in Main at In[5]:1 lineint(F::Vector{Sym}, c, a, b) in Main at In[17]:1 |
では、具体的に計算してみましょう。
1 2 3 4 5 | F1 = [y,x] for i in 1:5 display(lineint(F1,clist[i],0,1)) end |
\[ \begin{aligned}\left[ \begin{array}{r}y\\x\end{array} \right]\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
\[ \begin{aligned}1\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
\[ \begin{aligned}1\end{aligned} \]
\[ \begin{aligned}1\end{aligned} \]
端点が同じで、異なる経路によって線積分した結果を比べてみましょう。
1 2 3 4 | (lineint(F1,c1,0,1) +lineint(F1,c2,0,1) == lineint(F1,c3,0,1) +lineint(F1,c4,0,1) ) (lineint(F1,c1,0,1) +lineint(F1,c2,0,1) == lineint(F1,c5,0,1) ) |
1 2 | true true |
このベクトル場は、ポテンシャル関数を持ち、経路によって線積分の値が変わらないことが知られています。
別の例で計算してみます。
1 2 3 4 5 | F2 = [y, -x] for i in 1:5 display(lineint(F2,clist[i],0,1)) end |
\[ \begin{aligned}\left[ \begin{array}{r}y\\- x\end{array} \right]\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
\[ \begin{aligned}-1\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
\[ \begin{aligned}1\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
再び、同じ端点で異なる経路だと、線積分の結果が変わるかチェックしてみます。
1 2 | (lineint(F2,c1,0,1) +lineint(F2,c2,0,1) == lineint(F2,c5,0,1) ) |
1 | false |
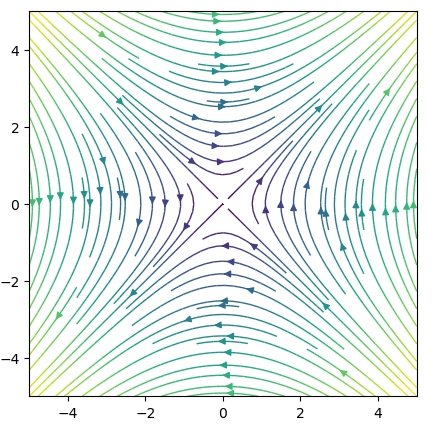
今度のベクトル場は、経路によって線積分の値が変わるので、ポテンシャル関数を持たないことがわかりました。
以上、Julia(SymPy)でスカラー場・ベクトル場の線積分を計算する方法を紹介してきました。
一度関数を定義してしまえば、いろいろな経路での計算が簡単にできて嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(PyPlot)で2次元のベクトル場・流線を描く方法