どうも、木村(@kimu3_slime)です。
今回は、Julia(Plots)で二次曲線(円、楕円、双曲線)を陰関数として描く方法を紹介します。
準備
Plots、ImplicitPlotsを使うので、持っていなければインストールしておきましょう。
1 2 | Pkg.add("Plots") Pkg.add("ImplicitPlots") |
準備として、以下のコードを実行しておきます。
1 | using Plots, ImplicitPlots |
二次曲線(円、楕円、双曲線)を陰関数として描く方法
円の方程式
\[ \begin{aligned}x^2+y^2 =4\end{aligned} \]
は、\(y\)について陽に解けていないので、普通の方法ではそのままグラフにはできません。しかし、
\[ \begin{aligned}f(x,y)= x^2 +y^2 -4\end{aligned} \]
という陰関数の形のまま、\(f(x,y)=0\)を満たす\((x,y)\)をそのままプロットすることができます。
1 2 | f(x,y) = x^2 + y^2 -4 implicit_plot(f) |
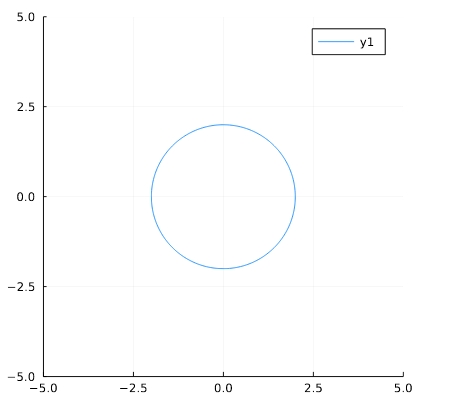
\(x^2+y^2 =c\)の形の方程式を、\(x^2+y^2 -c=0\)と左辺に寄せて定義していることに注意しましょう。
楕円
\[ \begin{aligned}\frac{x^2}{4} + y^2 -4=0\end{aligned} \]
も同様です。
1 2 | f(x,y) = x^2/4 + y^2 -4 implicit_plot(f) |

双曲線
\[ \begin{aligned}x^2- y^2 -4=0\end{aligned} \]
1 2 | f(x,y) = x^2 - y^2 -4 implicit_plot(f; xlims=(-10,10), ylims=(-10,10)) |
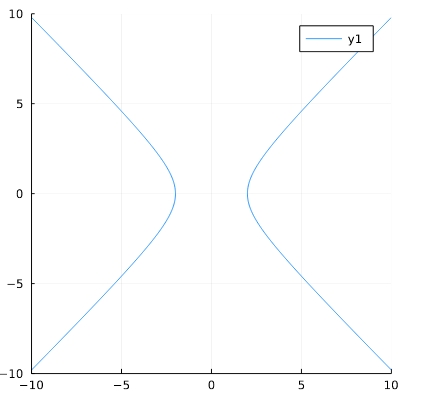
「xlims、ylims」によって描写する範囲を指定しています。
二次曲線以外の代数曲線の例として、楕円曲線
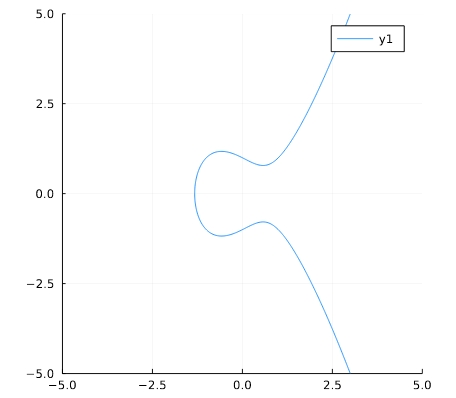
\[ \begin{aligned}y^2 =x^3 -x \end{aligned} \]
\[ \begin{aligned}y^2 =x^3 -x +1\end{aligned} \]
を描いてみましょう。
1 2 | f(x,y) = x^3 -x - y^2 implicit_plot(f) |
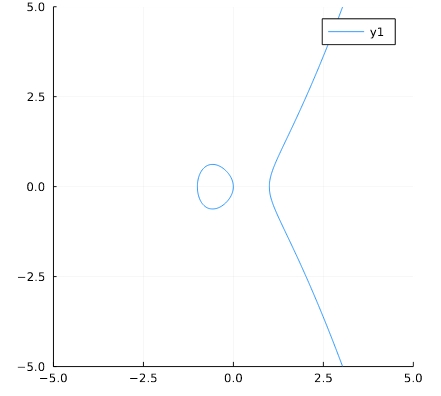
1 2 | f(x,y) = x^3 -x - y^2 + 1 implicit_plot(f) |
以上、Julia(Plots)で二次曲線(円、楕円、双曲線)を陰関数として描く方法を紹介してきました。
この方法では、曲面のような3次元のグラフを描くことはできません。しかし、曲線のパラメータ表示を知らなくても、陰関数方程式さえあればプロットできるのは便利ですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(Plots)でパラメータ付けられた曲面を描く方法
Julia(SymPy)でパラメータ付けられた曲線(平面、空間)を描く方法