どうも、木村(@kimu3_slime)です。
今回は、Julia(Plots)でパラメータ付けられた曲面を描く方法を紹介します。
前提知識:曲面のパラメータ表示、曲面積、球座標(3次元極座標)とは?
準備
Plots、PlotlyJSを使うので、持っていなければインストールしておきましょう。
1 2 | Pkg.add("Plots") Pkg.add("PlotlyJS") |
準備として、以下のコードを実行しておきます。
1 2 | using Plots plotlyjs() |
パラメータ付けられた曲面を描く方法
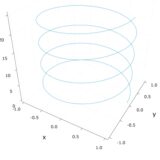
半径1の球面のパラメータ表示は
\[ \begin{aligned}x=\sin \theta \cos\phi ,y= \sin \theta \sin \phi,z= \cos \theta\end{aligned} \]
、\(0\leq \theta \leq \pi , 0 \leq \phi < 2\pi\)です。これを描いてみましょう。
1 2 3 4 5 6 7 | n=100 θ = range(0, pi ; length = n) φ = range(0, 2*pi; length = n) x = [cos(φ)*sin(θ) for θ in θ, φ in φ] y = [sin(φ)*sin(θ) for θ in θ, φ in φ] z = [cos(θ) for θ in θ, φ in φ] surface(x, y, z) |

パラメータ\(\theta ,\phi\)を、\(n\)分割した点において値を計算します。\(x,y,z\)は、各\(\theta, \phi\)における値を集めた配列です。それらを「surface」によって描く、という流れになっています。
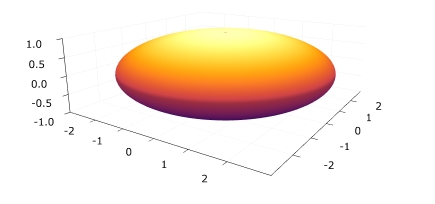
球面のパラメータ表示を、特定の方向へ拡大縮小すれば、楕円体となります。
1 2 3 4 5 6 7 | n=100 θ = range(0, pi ; length = n) φ = range(0, 2*pi; length = n) x = [3*cos(φ)*sin(θ) for θ in θ, φ in φ] y = [3*sin(φ)*sin(θ) for θ in θ, φ in φ] z = [cos(θ) for θ in θ, φ in φ] surface(x, y, z) |
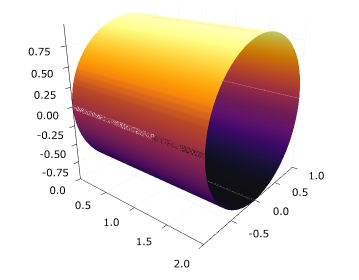
円筒を描くには、\(x= \phi\)、\(y= \cos \theta, \, z= \sin \theta\)のようにすれば良いです。
1 2 3 4 5 6 7 | n=100 θ = range(0, 2*pi ; length = n) φ = range(0, 2; length = n) x = [φ for θ in θ, φ in φ] y = [cos(θ) for θ in θ, φ in φ] z = [sin(θ) for θ in θ, φ in φ] surface(x, y, z) |
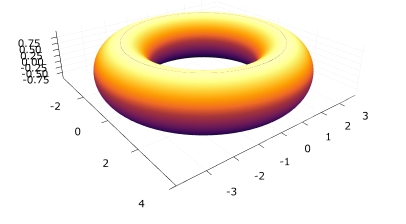
トーラス(ドーナツ型の図形)は、
\[ \begin{aligned}x=(R+r\cos u)\cos v\end{aligned} \]
\[ \begin{aligned}y=(R+r\cos u)\sin v\end{aligned} \]
\[ \begin{aligned}z=r \sin u\end{aligned} \]
\[ \begin{aligned}0 \leq u,v < 2\pi\end{aligned} \]
と表せます。\(r\)が管の太さ、\(R\)がトーラス全体の中心から管の中心への距離です。
1 2 3 4 5 6 7 | n=100 u = range(0, 2*pi ; length = n) v = range(0, 2*pi; length = n) x = [(3+cos(u))*cos(v) for u in u, v in v] y = [(3+cos(u))*sin(v) for u in u, v in v] z = [sin(u) for u in u, v in v] surface(x, y, z) |
以上、Julia(SymPy)でパラメータ付けられた曲面を描く方法を紹介してきました。
曲面を手描きするのは難しいので、コンピュータで描けると嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(SymPy)でパラメータ付けられた曲線(平面、空間)を描く方法
Julia(Plotly)でグリグリ動かせる3Dグラフを作る方法