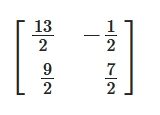どうも、木村(@kimu3_slime)です。
今回は、Julia(SymPy)で行列の正定値・負定値・不定値性を判定する方法を紹介します。
前提知識:2次形式、正定値行列とは:2変数関数の極値判定を例に
準備
SymPy、Plots、PlotlyJSを使うので、持っていなければインストールしておきましょう。
1 2 3 4 | using Pkg Pkg.add("SymPy") Pkg.add("Plots") Pkg.add("PlotlyJS") |
準備として、以下のコードを実行しておきます。
1 2 | using SymPy, Plots plotlyjs() |
参考:Julia(Plotly)でグリグリ動かせる3Dグラフを作る方法
行列の正定値・負定値・不定値性を判定する方法
「行列.is_positive_definite」で正定値かどうか、「行列.is_positive_semidefinite」で半正定値かどうかが調べられます。
1 2 3 | A = Sym[2 0; 0 2] A.is_positive_definite A.is_positive_semidefinite |
1 2 | true true |
Plotsを使って、この行列が定める2次形式\(x^{\top}Ax\)の3Dグラフを描いてみましょう。
1 2 | @vars x y (Sym[x,y].T * A *Sym[x,y])[1] |
\[ \begin{aligned}2 x^{2} + 2 y^{2}\end{aligned} \]
配列の中身を参照する[1]をつけないと、結果がSym型でなく、Vector{Sym}型になってしまいます。3Dグラフを描くsurfaceに与える関数は、Sym型の数式表現である必要があります。
1 2 3 | xs = ys = range(-5, 5, length=300) f(x, y) = (Sym[x,y].T * A *Sym[x,y])[1] surface(xs, ys, f,colorbar=false, alpha=0.9 ,xlabel = "x", ylabel = "y", zlabel = "f(x,y)") |
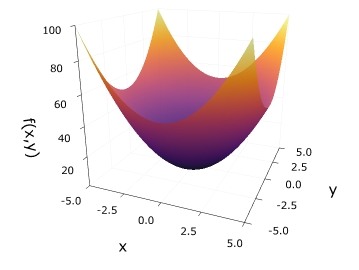
グラフからも、原点のみで値0を取り、他の点で正の値を取ることが読み取れますね。
「行列.is_negative_definite」で負定値かどうか、「行列.is_negative_semidefinite」で半負定値がわかります。
1 2 3 | B = Sym[-2 0; 0 0] B.is_negative_definite B.is_negative_semidefinite |
この例は、負定値ではありませんが、半不定値ではあります。
1 2 3 | xs = ys = range(-5, 5, length=300) f(x, y) = (Sym[x,y].T * B *Sym[x,y])[1] surface(xs, ys, f,colorbar=false, alpha=0.9 ,xlabel = "x", ylabel = "y", zlabel = "f(x,y)") |
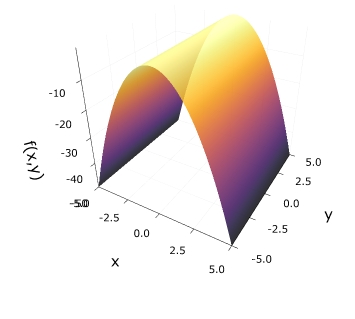
実際にグラフを見ると、値0を取っている点が原点だけでなく、\(x=0\)上にあることが読み取れます。
「行列.is_indefinite」で不定値行列かどうかの判定です。
1 2 | C = Sym[2 0; 0 -1] C.is_indefinite |
1 2 3 | xs = ys = range(-5, 5, length=300) f(x, y) = (Sym[x,y].T * C *Sym[x,y])[1] surface(xs, ys, f,colorbar=false, alpha=0.9 ,xlabel = "x", ylabel = "y", zlabel = "f(x,y)") |
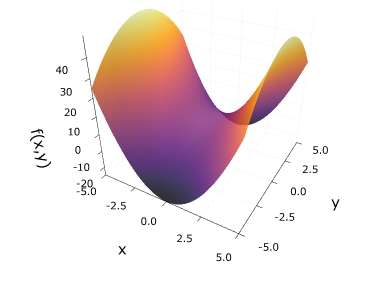
正の値を取る点と負の値を取る点が両方存在しており、不定値です。
2次の行列や、対称行列でなくても、定値性を判定することができます。
1 2 3 | D = Sym[1 2 3; 0 4 5; 6 7 0] D.is_positive_semidefinite D.is_negative_semidefinite |
\[ \begin{aligned}\left[ \begin{array}{rrr}1&2&3\\0&4&5\\6&7&0\end{array}\right]\end{aligned} \]
1 | @time D.is_indefinite |
1 | 0.004245 seconds (31 allocations: 1.531 KiB) |
3次の例では、「is_indefinite」でなぜか不定値かどうかを判定してくれません(処理は終わっているようだが、何も結果が表示されない)。
しかし、上で見た結果が正しいなら、半正定値でも半負定値でもないので、(定義から)不定値行列と判定できています。
(他のいくつかの3次の行列に対してis_indefiniteを試しましたが、機能したのは、対称行列かつ固有値が明確に求められる例のみでした。)
以上、Julia(SymPy)で行列の正定値・負定値・不定値性を判定する方法を紹介してきました。
限界はあるものの、ある程度の範囲で機械的に判定できるので、ぜひ活用してみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(Plotly)でグリグリ動かせる3Dグラフを作る方法