どうも、木村(@kimu3_slime)です。
今回は、Julia(SymPy)で常微分方程式の厳密解(解析解)を計算する方法を紹介します。
準備
SymPyを使うので、持っていなければインストールしておきましょう。
1 2 | using Pkg Pkg.add("SymPy") |
準備として、以下のコードを実行しておきます。
1 | using SymPy |
常微分方程式の厳密解を計算する方法
\(t\)を変数とする関数\(x(t)\)について考えたいと思います。\(x\)を関数として用意するためには「SymFunction(“文字”)」を使います。
1 2 | t = symbols("t") x = SymFunction("x") |
1階常微分方程式
最も簡単なケースとして、マルサスの法則の方程式を解きましょう。
「Eq(左辺,右辺)」で方程式が作れます。微分は「x'(t)」や「diff(x,t)」で表せます。
1 | Eq(x'(t),2*x(t)) |
\[ \begin{aligned}\frac{d}{d t} x{\left(t \right)} = 2 x{\left(t \right)}\end{aligned} \]
微分方程式を解くには、「dsolve(方程式)」です。
1 | dsolve(Eq(x'(t),2*x(t))) |
\[ \begin{aligned}x{\left(t \right)} = C_{1} e^{2 t}\end{aligned} \]
定数\(C_1\)を含む形で、きちんと一般的な解が得られました。
さらに、初期値問題を解いてみましょう。\(x(0)=x_0\)を満たす解を求めるには、「dsolve(方程式, ics=(x,0,x0))」です。
1 | dsolve(Eq(x'(t),2*x(t)), x(t), ics = (x,0,3) ) |
\[ \begin{aligned}x{\left(t \right)} = 3 e^{2 t}\end{aligned} \]
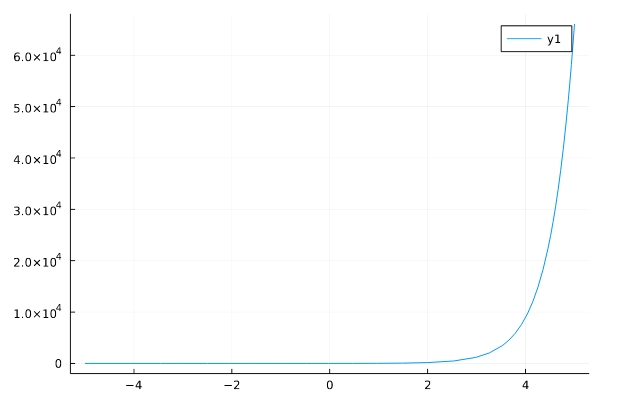
Plotsを使って、グラフを描くこともできます。「rhs(方程式)」で、方程式の右辺、つまり微分方程式の解が取り出せます。それをプロットしましょう。
1 2 3 | using Plots rhs(dsolve(Eq(x'(t),2*x(t)), x(t), ics = (x,0,3) )) plot(rhs(dsolve(Eq(x'(t),2*x(t)), x(t), ics = (x,0,3) ))) |
\[ \begin{aligned}3 e^{2 t}\end{aligned} \]
1 2 | Eq(x'(t),x(t)- (x(t))^2) dsolve(Eq(x'(t),x(t)- (x(t))^2)) |
\[ \begin{aligned}\frac{d}{d t} x{\left(t \right)} = – x^{2}{\left(t \right)} + x{\left(t \right)}\end{aligned} \]
\[ \begin{aligned}x{\left(t \right)} = \frac{1}{C_{1} e^{- t} + 1}\end{aligned} \]
きちんと解けています。
2階常微分方程式
2回微分は「x”(t)」で表せます。
1 2 | Eq(x''(t), -1) dsolve(Eq(x''(t),-1)) |
\[ \begin{aligned}\frac{d^{2}}{d t^{2}} x{\left(t \right)} = -1\end{aligned} \]
\[ \begin{aligned}x{\left(t \right)} = C_{1} + C_{2} t – \frac{t^{2}}{2}\end{aligned} \]
\(x(0)=x_0, x^{\prime}(0)=v_0\)を満たす解を求めてみましょう。複数の初期値を指定するには、「ics=(条件1,条件2)」といった形にする必要があります。
1 | dsolve(Eq(x''(t),-x(t)), ics =((x,0,x0),(x',0,v0)) ) |
\[ \begin{aligned}x{\left(t \right)} = – \frac{t^{2}}{2} + t v_{0} + x_{0}\end{aligned} \]
1 2 3 | Eq(x''(t),-x(t)) dsolve(Eq(x''(t),-x(t))) dsolve(Eq(x''(t),-x(t)), ics =((x,0,x0),(x',0,v0)) ) |
\[ \begin{aligned}\frac{d^{2}}{d t^{2}} x{\left(t \right)} = – x{\left(t \right)}\end{aligned} \]
\[ \begin{aligned}x{\left(t \right)} = C_{1} \sin{\left(t \right)} + C_{2} \cos{\left(t \right)}\end{aligned} \]
\[ \begin{aligned}x{\left(t \right)} = v_{0} \sin{\left(t \right)} + x_{0} \cos{\left(t \right)}\end{aligned} \]
非同次(非斉次)の微分方程式も解いてくれます。
1 2 3 4 | Eq(x''(t),-x(t)-cos(2*t)) dsolve(Eq(x''(t),-x(t)-cos(2*t))) Eq(x''(t),-x(t)-cos(t)) dsolve(Eq(x''(t),-x(t)-cos(t))) |
\[ \begin{aligned}\frac{d^{2}}{d t^{2}} x{\left(t \right)} = – x{\left(t \right)} – \cos{\left(2 t \right)}\end{aligned} \]
\[ \begin{aligned}x{\left(t \right)} = C_{1} \sin{\left(t \right)} + C_{2} \cos{\left(t \right)} + \frac{\cos{\left(2 t \right)}}{3}\end{aligned} \]
\[ \begin{aligned}\frac{d^{2}}{d t^{2}} x{\left(t \right)} = – x{\left(t \right)} – \cos{\left(t \right)}\end{aligned} \]
\[ \begin{aligned}x{\left(t \right)} = C_{2} \cos{\left(t \right)} + \left(C_{1} – \frac{t}{2}\right) \sin{\left(t \right)}\end{aligned} \]
前者がうなり、後者が共鳴です。
ここまで厳密に解けるものを紹介してきましたが、dsolveは万能ではありません。
1 2 | Eq(x''(t),-sin(x(t))) dsolve(Eq(x''(t),-sin(x(t)))) |
\[ \begin{aligned}\frac{d^{2}}{d t^{2}} x{\left(t \right)} = – \sin{\left(x{\left(t \right)} \right)}\end{aligned} \]
は、長い時間をかけても結果を返してくれませんでした。
以上、Julia(SymPy)で常微分方程式の厳密解を計算する方法を紹介してきました。
微分方程式のコンピュータでの計算というと数値計算のイメージがありますが、SymPyは記号的に解ける範囲では十分に解いてくれるので嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Juliaで1変数関数のグラフを描く方法(多項式、指数対数、三角関数)
Julia(SymPy)によるテイラー級数展開の求め方(指数対数、三角、双曲線)
Julia(SymPy)で1変数関数を積分する方法(多項式、指数対数、三角関数)
Julia(SymPy)で1変数関数を微分する方法(多項式、指数対数、三角関数)