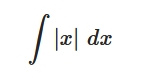どうも、木村(@kimu3_slime)です。
今回は、Julia(SymPy)で1変数関数の極限を求める方法を紹介します。
準備
SymPyを使うので、持っていなければインストールしておきましょう。
1 2 | using Pkg Pkg.add("SymPy") |
準備として、以下のコードを実行しておきます。
1 | using SymPy |
1変数関数の極限
まず、\(x\)を数式処理用の変数、記号として用意しましょう。
1 | x=symbols("x") |
単純な関数の極限
「limit(関数,変数,値)」で極限を求めることができます。
1 | limit(x,x,0) |
\[ \begin{aligned}0\end{aligned} \]
これは、\(\lim_{x\to 0}x =0\)を意味しています。確かにその通りです。
無限大\(\infty\)に近づけるときは、値として2つのオー「oo」を用いれば良いです。
1 | limit(x,x,oo) |
\(\frac{1}{x}\)の\(x\to \infty\)での極限値も、きちんと計算できます。
1 | limit(1/x,x, oo) |
\[ \begin{aligned}0\end{aligned} \]
\(\lim_{x\to 0} \frac{1}{x}\)はどうでしょうか。
1 | limit(1/x,x, 0) |
\[ \begin{aligned}0\end{aligned} \]
右側極限を考えるときは、
1 | limit(1/x,x, 0,"+") |
\[ \begin{aligned}\infty\end{aligned} \]
とオプションを加えましょう。「”+”」を書かない場合、デフォルトでは右側極限と解釈されます(ただし、正の無限大では左側極限を考えている)。
マイナスに変えることで、左側極限を考えることができます。
1 | limit(1/x,x, 0,"-") |
\[ \begin{aligned}-\infty\end{aligned} \]
両側極限を考えるためには、オプションを「”+-“」にすれば良いです。
1 2 | x = symbols("x", real = True) limit(1/x,x, 0,"+-") |
\[ \begin{aligned}\tilde{\infty}\end{aligned} \]
\(\tilde{\infty}\)(zoo)は、複素無限遠点を表す記号です。複素無限遠点を考えると、\(\infty ,-\infty\)といった極限値もひとつの点として扱えるので、このように書かれるわけです。
しかし、実数の極限としてこの結果が表示されるのは、微妙な仕様ですね。\(\lim_{x\to 0} \frac{1}{x}\)では、実数の(両側)極限は存在しません。「NaN」を返してほしいです。
\(\frac{x}{x}\)の極限は、どうなるでしょうか。
1 | limit(x/x ,x ,0) |
\[ \begin{aligned}1\end{aligned} \]
数式はあらかじめ単純化され、\(\frac{0}{0}\)、不定形とならないように解釈されています。
1次関数の比\(\lim_{x\to \infty}\frac{2x+1}{x}\)
1 | limit((2*x+1)/x ,x ,oo) |
\[ \begin{aligned}2\end{aligned} \]
最高次の係数の比になっていますね。
振動する関数\(\lim_{x\to\infty}(-1)^x\)
1 | limit((-1)^x ,x,oo) |
\[ \begin{aligned}\text{NaN}\end{aligned} \]
\(\text{NaN}\)はNot a Numberの略で、数でない、つまり極限が存在しないことを意味しています。
微積分における基本的な極限
オイラー数(ネイピア数)\(e\)の定義式\(\lim_{x\to \infty} (1+\frac{1}{x})^x\)からは、きちんと\(e\)が導かれます。
1 | limit((1+1/x)^x ,x,oo) |
\[ \begin{aligned}e\end{aligned} \]
初等関数と1次関数の比較、接線近似の極限
\[ \begin{aligned}\lim_{x \to 0}\frac{\sin x}{x} =1\end{aligned} \]
\[ \begin{aligned}\lim_{x \to 0}\frac{\cos x -1}{x} =0\end{aligned} \]
\[ \begin{aligned}\lim_{x \to 0}\frac{e^x -1}{x} =1\end{aligned} \]
\[ \begin{aligned}\lim_{x \to 0}\frac{\log _e (1+x)}{x} =1\end{aligned} \]
の結果も導けます。
1 2 3 4 | limit(sin(x)/x,x,0) limit((cos(x)-1)/x,x,0) limit((exp(x)-1)/x,x,0) limit(log(x+1)/x ,x,0) |
\[ \begin{aligned}1\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
\[ \begin{aligned}1\end{aligned} \]
\[ \begin{aligned}1\end{aligned} \]
参考:有名な極限の公式f(x)/xの覚え方:接線近似とテイラー展開
対数関数、多項式、指数関数、階乗の無限大での増大スピードの比較も得られます。
\[ \begin{aligned}\lim_{x\to \infty} \frac{\log_e x}{x^a}= 0\end{aligned} \]
\[ \begin{aligned}\lim_{x\to \infty} \frac{x^a}{x^b}= 0\end{aligned} \]
\[ \begin{aligned}\lim_{x\to \infty} \frac{x^b}{e^x}= 0\end{aligned} \]
\[ \begin{aligned}\lim_{x\to \infty} \frac{e^x}{x!}= 0\end{aligned} \]
1 2 3 4 | limit(log(x)/x^2,x,oo) limit(x^2/x^3,x,oo) limit(x^3/exp(x),x,oo) limit(exp(x)/factorial(x),x,oo) |
\[ \begin{aligned}0\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
関数の微分も、微分の極限による定義にしたがって計算できます。
\[ \begin{aligned}\lim_{h\to 0} \frac{(x+h)^3 -x^3}{h}\end{aligned} \]
1 2 | h = symbols("h") limit(((x+h)^3-x^3)/h,h,0,"+-") |
\[ \begin{aligned}3x^2\end{aligned} \]
考えている変数が\(h\)に変わったことに注意しましょう。
参考:Julia(SymPy)で1変数関数を微分する方法(多項式、指数対数、三角関数)
以上、Julia(SymPy)で1変数関数の極限を求める方法を紹介してきました。
コンピュータにおいても無限大や極限を扱えるのは便利ですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(SymPy)で1変数関数を微分する方法(多項式、指数対数、三角関数)
.Julia(SymPy)で有理関数を部分分数分解、通分する方法
Julia(SymPy)で多項式の展開・因数分解、方程式を解く方法
Juliaで1変数関数のグラフを描く方法(多項式、指数対数、三角関数)