どうも、木村(@kimu3_slime)です。
今回は、Julia(SymPy)で多項式の展開・因数分解、方程式を解く方法を紹介します。
準備
SymPyを使うので、持っていなければインストールしておきましょう。
1 2 | using Pkg Pkg.add("SymPy") |
準備として、以下のコードを実行しておきます。
1 | using SymPy |
多項式の展開・因数分解、方程式の解き方
1次多項式、方程式
まず、変数として利用する記号を宣言する必要があります。例えば次のように。
1 | x=symbols("x") |
「@vars x」といった表現でも可能です。
Jupyter notebookならば、
\[ \begin{aligned}x\end{aligned} \]
というLaTeX形式の数式が返ってきます。
1次多項式を定義してみましょう。
1 | ex = 5*x+2 |
結果は「\(5 x + 2\)」となります。\(x\)に特定の値を代入(数値計算)せず、記号としてそのまま扱えている(数式処理)のがポイントです。
さて、この1次多項式により定まる
\[ \begin{aligned}5x+2=0\end{aligned} \]
という1次方程式を解いてみましょう。「solve(数式,変数)」という関数を用います。
1 | solve(ex,x) |
\[ \begin{aligned}\left[ \begin{array}{r}- \frac{2}{5}\end{array} \right]\end{aligned} \]
と、確かに解が求まりました。
1次多項式に、特定の値を代入した結果も求められます。試しに、\(x= -\frac{2}{5}\)を代入してみましょう。「数式.subs(変数,代入する値)」です。
1 | ex.subs(x, -2/5) |
\[ \begin{aligned}0\end{aligned} \]
結果は0で、確かに方程式を解けていることがわかりました。
より一般的な形として、係数を記号で置いたまま、1次方程式を解くこともできます。新たに記号\(a,b\)を導入しましょう。
1 2 3 | a,b =symbols("a b") ex2 = a*x+b solve(ex2,x) |
\[ \begin{aligned}a x + b\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}- \frac{b}{a}\end{array} \right]\end{aligned} \]
確かに、1次方程式が一般的な形で解けていますね。
方程式は何を変数として解くかによって、その解は変わります。\(x\)でなく\(b\)を変数として見るならば、
1 | solve(ex2,b) |
\[ \begin{aligned}\left[ \begin{array}{r}- a x\end{array} \right]\end{aligned} \]
と\(b= \)の形で解くこともできるわけです。
2次以上の多項式、方程式
2次以上の多項式について、考えてみましょう。
多項式の積の形の数式を定義し、それを展開することもできます。「expand(数式)」です。
1 2 | ex3 = (x-2)*(x-3) expand(ex3) |
\[ \begin{aligned}\left(x – 3\right) \left(x – 2\right)\end{aligned} \]
\[ \begin{aligned}x^{2} – 5 x + 6\end{aligned} \]
逆に、多項式を因数分解する(1次多項式の積として表す)こともできます。
1 2 | ex4 = expand(ex3) factor(ex4) |
\[ \begin{aligned}x^{2} – 5 x + 6\end{aligned} \]
\[ \begin{aligned}\left(x – 3\right) \left(x – 2\right)\end{aligned} \]
当然ですが、因数分解は2次方程式を解いた結果と対応しています。
1 | solve(ex4) |
\[ \begin{aligned}\left[ \begin{array}{r}2\\3\end{array} \right]\end{aligned} \]
ただし、SymPyの因数分解には限界があります。
まず、解が無理数となる場合、因数分解されません。「factor」しても、元の2次多項式が返ってきます。
1 2 3 | ex7 = x^2 - 2 factor(ex7) solve(ex7) |
\[ \begin{aligned}x^{2} – 2\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}- \sqrt{2}\\\sqrt{2}\end{array} \right]\end{aligned} \]
solveを使えば、きちんと\(\pm \sqrt{2}\)という解がそのまま返ってきます。
ちなみに、無理数を小数を使って近似表示することもできます。「数式.evalf()」です。
1 | solve(ex7).evalf() |
\[ \begin{aligned}\left[ \begin{array}{r}-1.4142135623731\\1.4142135623731\end{array}\right]\end{aligned} \]
また、解が虚数となる場合も、因数分解されません。ただし、解はきちんと複素数の範囲で求められます。
1 2 3 | ex6 = x^2+1 factor(ex6) solve(ex6) |
\[ \begin{aligned}x^{2} + 1\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}- i\\i\end{array} \right]\end{aligned} \]
より高次の多項式も、解が有理数となる場合は因数分解できます。手計算だと難しいことがあるので、これは便利ですね。
1 2 | ex5 = 3*x^3 - 2*x^2 -12*x + 8 factor(ex5) |
\[ \begin{aligned}3 x^{3} – 2 x^{2} – 12 x + 8\end{aligned} \]
\[ \begin{aligned}\left(x – 2\right) \left(x + 2\right) \left(3 x – 2\right)\end{aligned} \]
1 2 | ex8 = x^5 - 5*x^3 + 4*x factor(ex8) |
\[ \begin{aligned}x^5 -5x^3+4x\end{aligned} \]
\[ \begin{aligned}x \left(x – 2\right) \left(x – 1\right) \left(x + 1\right) \left(x + 2\right)\end{aligned} \]
Plotsを使うことで、多項式を関数として見たときのグラフを描くこともできます。
1 2 | using Plots plot(ex8, xlim=(-2.1,2.1)) |
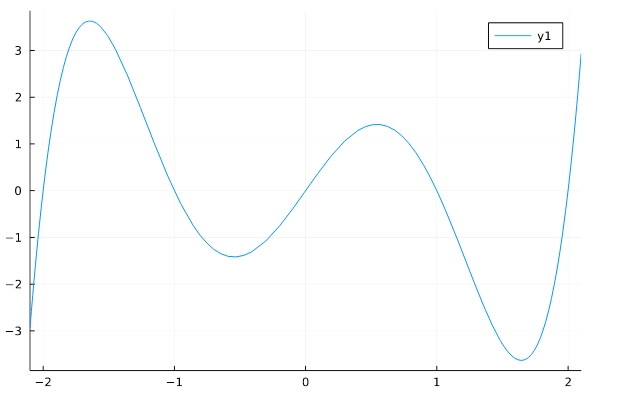
確かに解が\(x=-2,-1,0,1,2\)にありますね。
二項展開
文字のまま多項式を展開できるので、それを使って\((a+b)^n\)の展開(二項展開)を求めてみましょう。
新たに変数\(n\)を導入し、\(n=1,2,\dots,5\)のケースを配列として返してみます。
1 2 3 | n=symbols("n") ex9 = (a+b)^n [expand(ex9.subs(n,i)) for i in 1:5] |
\[ \begin{aligned}\left[ \begin{array}{r}a + b\\a^{2} + 2 a b + b^{2}\\a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}\\a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}\\a^{5} + 5 a^{4} b + 10 a^{3} b^{2} + 10 a^{2} b^{3} + 5 a b^{4} + b^{5}\end{array} \right]\end{aligned} \]
二項係数が登場しているのが見て取れますね。例えば\(n=100\)のケースを0.000183秒で求めることもできて、

となります(笑)。少なくとも\(C(100,0)=1\)、\(C(100,1)=1\)がわかりますね。
以上、Julia(SymPy)で多項式の展開・因数分解、方程式を解く方法を紹介してきました。
普通の電卓では多項式の展開や因数分解をすることはできませんが、SymPyを使えば比較的簡単です。もちろん手計算に慣れるのも大事ですが、コンピュータで求める方法も知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Juliaで1変数関数のグラフを描く方法(多項式、指数対数、三角関数)