どうも、木村(@kimu3_slime)です。
今回は、複素ポテンシャルの実部、虚部の等高線が直交することの証明を紹介します。
静電ポテンシャルを例とするならば、等電位線と電気力線が直交する理由になっています。
調和関数(実ポテンシャル)\(\Phi\)とその共役調和関数によって、
\[ \begin{aligned}F(z):=\Phi +i \Psi\end{aligned} \]
と表せる複素関数は、複素ポテンシャルと呼ばれます。
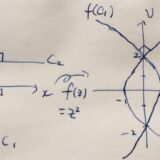
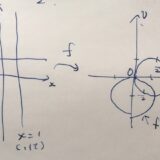
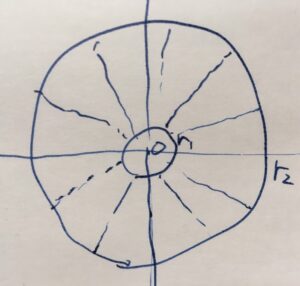
例えば、円環領域における\(\Phi (x,y)=a \log r +b\)というポテンシャルに対し、共役調和関数は\(\Psi = a \mathrm{Arg} z\)で、\(F(z) = a\mathrm{\,Log} z +b\)となります。
それぞれの等高線は円、原点を中心とした放射状の直線となり、直交していることがわかります。
議論の出発点を変えて、\(F\)を正則関数と考えても、その実部、虚部は調和関数となっているので、以降で同様の議論ができます。つまり、正則関数の実部、虚部の等高線は直交します。
一般に、実部と虚部の等高線(等ポテンシャル曲線)\(\Phi(x,y) = K_1\)と\(\Psi(x,y) = K_2\)が直交する理由を説明しましょう。
\(\Phi ,\Psi \)はコーシー・リーマンの方程式を満たすように定めたので、
\[ \begin{aligned}\Phi_x =\Psi _y\end{aligned} \]
\[ \begin{aligned}\Phi_y =-\Psi _x\end{aligned} \]
を満たします。また、等高線の法線ベクトルは、勾配ベクトルとして表されます。それぞれの内積を計算すると、
\[ \begin{aligned}\langle \nabla \Phi, \nabla \Psi\rangle\\ =\Phi_x \Psi _x +\Phi_y \Psi _y \\ =-\Phi_x \Phi_y + \Phi_y \Phi_x\\ =0\end{aligned} \]
となり、\(\nabla \Phi ,\nabla \Psi \neq 0\)ならば、法線ベクトルが直交しています。したがって、等高線自身も直交することがわかりました。
別の方法で示すこともできます。
複素ポテンシャル\(F\)は正則関数であり、\(F^{\prime}(z) \neq 0\)となる点では\(F\)は等角写像です。また、一般に等角写像の逆写像も等角写像です。
\(F(z)\)の実部、虚部を\((u,v)\)と表すことにしましょう。すると、等高線の像\(\Phi(x,y) = K_1\)とは\(u=K_1\)、\(\Psi(x,y) = K_2\)とは\(v=K_2\)という直線です。これらは\((u,v)\)座標において直交しています。

したがって、等高線\((x,y)=\Phi ^{-1}(K_1)\)と\((x,y)=\Psi^{-1}(K_2)\)は直交することがわかりました。
以上、複素ポテンシャルの実部、虚部の等高線が直交することの証明を紹介してきました。
コーシー・リーマンの方程式から導かれる基本的な性質として理解すると良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Kreyszig, E: Advanced Engineering Mathematics
Wiley John + Sons (2011-05-03T00:00:01Z)
¥10,314 (中古品)
岩波書店 (2003-12-12T00:00:01Z)
¥2,640
日本評論社 (2009-06-01T00:00:01Z)
¥5,170
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740
こちらもおすすめ
勾配ベクトルが等位曲面に垂直である(法線ベクトル):例と証明