どうも、木村(@kimu3_slime)です。
今回は、Juliaで級数を計算し、グラフを描く方法を紹介します。
Plotsのインストール
グラフ描写用のパッケージ、Plotsをインストールしておきましょう。既にインストールしてある場合、飛ばしてください。
1 2 | using Pkg Pkg.add("Plots") |
有限和・無限級数
準備として、Plotsを使えるようにしておきましょう。
1 | using Plots |
自然数の4乗の和を20項まで計算してみます。
\[ \begin{aligned}\sum_{n=1}^{20} n^4\end{aligned} \]
1 2 3 4 5 6 7 8 9 10 | function f_1(N) s=0 for n in 1:N s+= n^4 end return s end x=[f_1(N) for N in 1:20] bar(x) |
関数として級数を定義しました。初期値をs=0として、「s+= n^4」によってsに\(n^4\)を1から指定したNのときまで足していき、その内容を返す関数です。n^4の部分を変えれば、他の数列の和が求められます。
後半では級数の値を数列、配列として見て、棒グラフに描きました。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | 20-element Array{Int64,1}: 1 17 98 354 979 2275 4676 8772 15333 25333 39974 60710 89271 127687 178312 243848 327369 432345 562666 722666 |
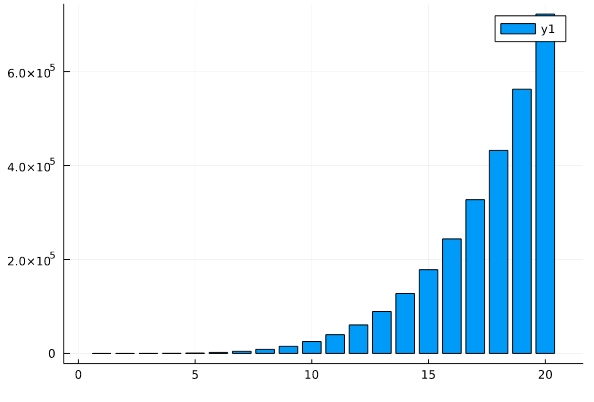
級数の計算は、sumを使って
1 | sum(n^4 for n in 0:20) |
と簡単に描くこともできます。
1 2 3 | g(N)=sum(n^4 for n in 0:N) x=[g(N) for N in 0:20] bar(x) |
逆数の2乗和、無限級数
\[ \begin{aligned}\sum_{n=1}^{\infty} \frac{1}{n^2}\end{aligned} \]
を近似的に求めてみましょう。
1 2 3 4 5 6 7 8 9 10 | function f_2(N) s=0 for n in 1:N s+= 1/n^2 end return s end x=[f_2(N) for N in 1:10^3] plot(x) |
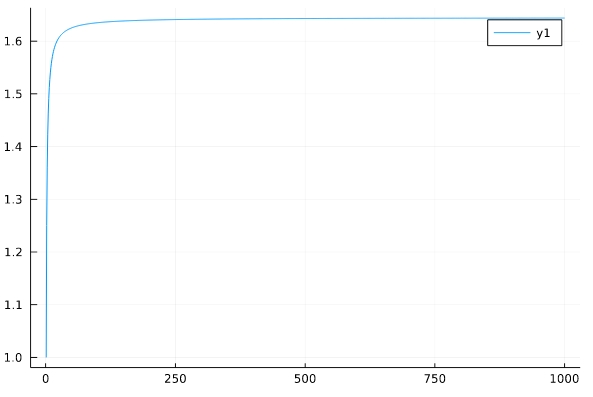
この級数の値は、\(\frac{\pi ^2}{6}\)であることが知られています。誤差を計算してみると
1 2 | println(f_2(10^3)) println(abs(f_2(10^3)- pi^2/6)) |
1 2 | 1.6439345666815615 0.0009995001666649461 |
となりました。
参考:負のべき乗の無限級数Σ1/n^pの収束・発散の判定方法
テイラー展開
関数のテイラー展開とそのグラフを描いてみましょう。
指数関数は
\[ \begin{aligned}e^{x}= \sum_{n=0}^\infty \frac{1}{n!}x^n\end{aligned} \]
です。\(x=1\)のときの値\(e\)は、さきほどの方法で求められます(試してみてください)。
テイラー展開のような関数項級数、\(x,N\)を変数とする関数を、2変数関数として定義しましょう。
1 2 3 4 5 6 7 8 9 | function f_3(x,N) s=1 for n in 1:N s+= 1/factorial(big(n)) * x^n end return s end plot(x->f_3(x,3)) |
「factorial(big(n))」で階乗\(n!\)を表しています。bigをつけているのは、オーバーフロー対策です。
「plot(x->f_3(x,3))」によって、3次までのテイラー展開のグラフを描いています。f_3には2つの変数がありますが、「x->f(x,N)」と書くことで、xを変数とする関数のグラフとして認識されます。
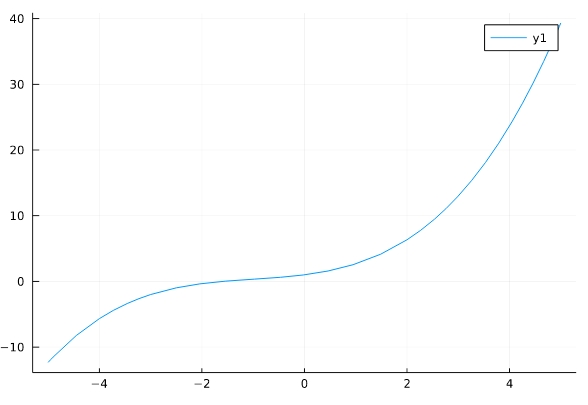
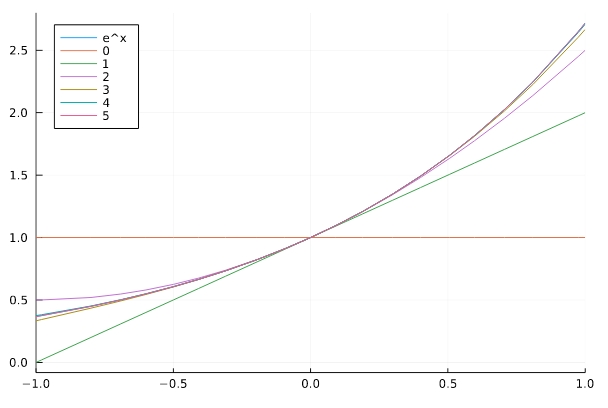
\(e^x\)と最初の5次までの項のグラフを、重ねて描いてみましょう。
1 2 3 4 5 6 | p = plot( xlim=(-1,1),legend=:topleft) plot!(p,x->exp(x) , label="e^x") for N in 0:5 plot!(p, x->f_3(x,N), label=string(N)) end plot(p) |
最初に、pとして何も書かれていないプロットの土台を作ります。ついで、そのpに他のプロットを「plot!」によって足していきました。plot!は破壊的な操作、pに新たなグラフを追加する操作です。for文を使うことで、0から5次までのグラフを順に追加しています。
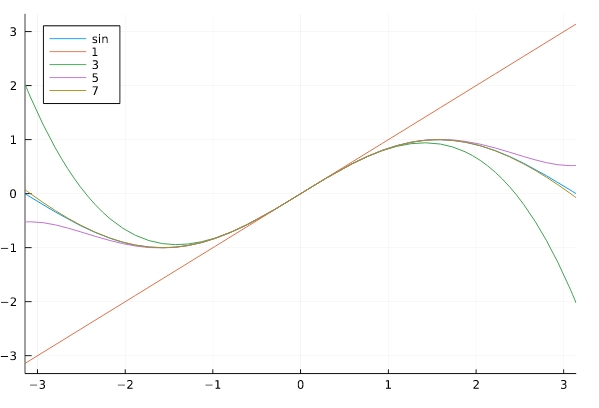
三角関数、サインのテイラー展開
\[ \begin{aligned}\sin x=x- \frac{x^3}{3!}+ \frac{x^5}{5!}- \cdots\\ = \sum_{n=0}^\infty \frac{(-1)^{n}}{(2n+1)!}x^{2n+1}\end{aligned} \]
も同様にして描いてみましょう。
1 2 3 4 5 6 7 8 9 10 11 12 | function f_4(x,N) s=0 for n in 1:N if n % 4 ==1 s+= 1/factorial(big(n)) * x^n elseif n % 4 ==3 s+= -1/factorial(big(n)) * x^n else end end return s end |
if文を使うことで、番号によって値の加え方を変えています。4で割ったあまりが1ならば\(\frac{1}{n!}x^n\)、4で割ったあまりが3ならば\(-\frac{1}{n!}x^n\)、それ以外ならば何もしません。
1 2 3 4 5 6 | p = plot( xlim=(-pi,pi),legend=:topleft) plot!(p,x->sin(x) , label="sin") for N in 1:2:7 plot!(p, x->f_4(x,N), label=string(N)) end plot(p) |
フーリエ級数展開
テイラー展開と同様にして、フーリエ級数展開を計算し、グラフを描くことができます。
\[ \begin{aligned}f(x)=\sum_{k=1}^\infty \frac{4}{(2k-1)\pi} \sin (2k-1)x\\ = \frac{4}{\pi}\sin x+ \frac{4}{3\pi} \sin 3x + \frac{4}{5\pi} \sin 5x +\cdots\end{aligned} \]
を描いてみましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | function f_5(x,N) s = 0 for n=1:N if n % 2 == 1 s +=4/(n*pi) *sin(n*x) else end end return s end p = plot(legend=:topleft, xlim=(-2*pi,2*pi),xticks=([-2pi,-pi, 0, pi, 2pi],["-2π", "-π", "0", "π","2π"])) plot!(p,x->sign.(sin.(x)) , label="square") for N in 1:2:5 plot!(p, x->f_5(x,N), label=string(N)) end plot!(p, x->f_5(x,1000), label=string(1000)) plot(p) |
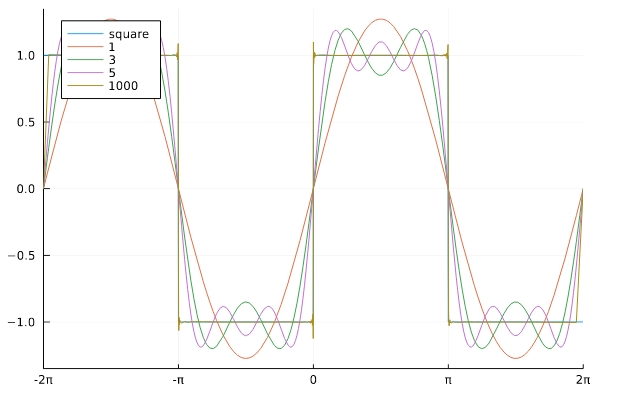
のこぎり波、三角波、絶対サイン波のグラフも同様にして描くことができます。ぜひ考えてみてください。
以上、Juliaで級数を計算し、グラフを描く方法を紹介してきました。
テイラー展開やフーリエ級数展開は、手計算で高次の項まで計算するのは大変です。コンピュータの力を使ってグラフを描くと、その威力をわかりやすく感じられるでしょう。
(SymPyを使うと、テイラー展開を代数的に求めることができるようです。別記事で紹介するかも。)
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
矩形波とは:フーリエ級数展開の求め方、ギブス現象、ライプニッツの級数