どうも、木村(@kimu3_slime)です。
今回は、のこぎり波とは何か、フーリエ級数展開の求め方を紹介します。
のこぎり波とは
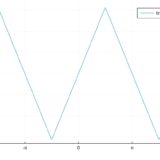
のこぎり波(sawtooth wave)は、のこぎりのようにギザギザとした次の図のような波です。
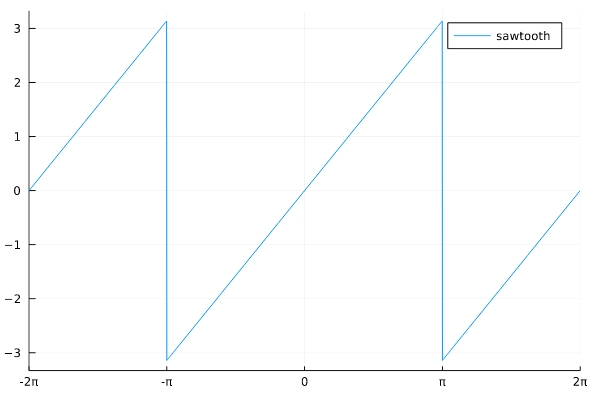
数学的には、
\[ \begin{aligned}f(x)= x\quad (-\pi < x <\pi)\end{aligned} \]
を周期\(2\pi\)の関数として周期的に拡張(\(f(x)=f(x+2n\pi)\))したものです。より明示的には、
\[ \begin{aligned}f(x)=x-2\pi \lfloor \frac{x}{2\pi}+\frac{1}{2}\rfloor\end{aligned} \]
と定義できます。ここで\(\lfloor x\rfloor\)は床関数(整数部分)です。
中身に注目すると、\(x= -\pi\)で\(\lfloor \frac{-\pi}{2\pi}+\frac{1}{2}\rfloor=0\)、\(x=\pi\)で\(\lfloor \frac{-\pi}{2\pi}+\frac{1}{2}\rfloor=1\)となっています。これにその周期における変化分\(2\pi\)をかけることで、周期\(2\pi\)ごとに値が\(2\pi\)だけ落ちる不連続な関数が作り出せています。
音として聞いてみるのも良いでしょう。矩形波と比べると、警告音・ビープ音というのか、濁った感じがします。
フーリエ級数展開の求め方
では、のこぎり波のフーリエ級数展開を求めてみましょう。
のこぎり波は奇関数なので、そのフーリエ級数展開は次のように簡単になります。
\[ \begin{aligned}f(x)=\sum_{n=1}^\infty b_n \sin nx\end{aligned} \]
\[ \begin{aligned}b_n = \frac{2}{\pi}\int_0^\pi f(x) \sin nx dx\end{aligned} \]
これを計算してみましょう。部分積分によって、
\[ \begin{aligned} b_n &= \frac{2}{\pi}\int_0^\pi x \sin nx dx \\ &=\frac{2}{\pi}([-\frac{1}{n}x\cos nx]_{0}^{\pi}+\frac{1}{n}\int_0^\pi \cos nx dx)\\ &=\frac{2}{\pi}(-\frac{\pi}{n}\cos n\pi+\frac{1}{n}[\frac{1}{n}\sin nx]_0 ^\pi)\\ &= -\frac{2}{n}\cos n\pi \\&= (-1)^{n-1}\frac{2}{n}\end{aligned} \]
と求められます。
フーリエ係数の分布、各周波数での三角関数\(\sin nx\)の成分の強さ・振幅を、スペクトルとして図示すると次のようになります。
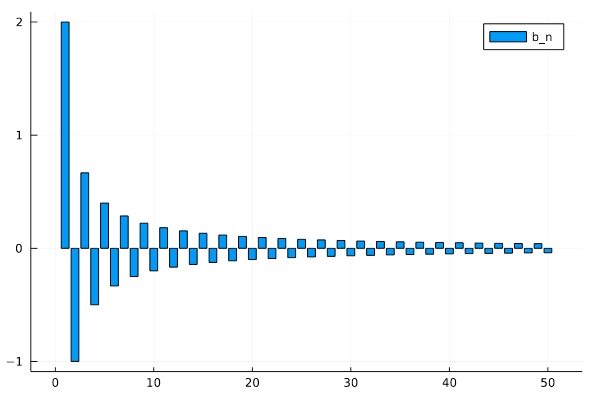
符号は正負に交代しながら、大きさは\(1/n\)で段々と小さくなっていきますね。
のこぎり波のフーリエ級数展開は次のようになりました。
\[ \begin{aligned}f(x)=\sum_{n=1}^\infty (-1)^{n-1} \frac{2}{n} \sin nx\\ = 2\sin x -\sin 2x + \frac{2}{3 }\sin 3x – \cdots\end{aligned} \]
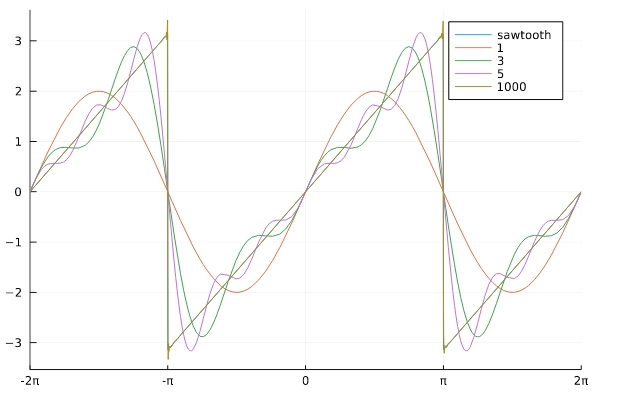
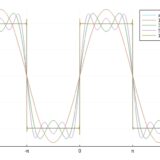
項数を増やすにつれ、きちんとのこぎり波に近づいていくのが見て取れます。
\(x= -\pi,\pi\)といった不連続点付近では、フーリエ級数にはトゲのようなものが見られ、これはギブス現象と呼ばれるものです。
フーリエ級数の不連続点での値は、元の関数の右極限と左極限の平均値、今回ならば\(\frac{-\pi +\pi}{2}=0\)に収束することが知られています。グラフともマッチしていますね。
以上、のこぎり波とは何か、そのフーリエ級数展開の求め方を紹介してきました。
矩形波に次いでシンプルな計算ができる関数なので、ぜひ自分でも計算してみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
Partial Differential Equations (Graduate Studies in Mathematics)
Amer Mathematical Society (2010-04-02T00:00:01Z)
¥9,531 (中古品)
こちらもおすすめ
矩形波とは:フーリエ級数展開の求め方、ギブス現象、ライプニッツの級数