1次元の非同次の移流方程式の解き方：特性曲線法

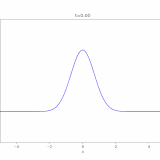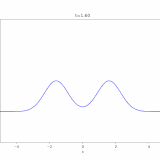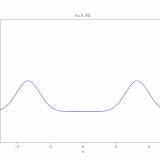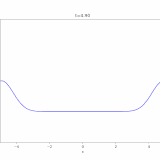
どうも、木村（@kimu3_slime）です。

今回は、1次元の非同次（非斉次）移流方程式（輸送方程式）の解き方を紹介します。

考える方程式は、

\[\begin{aligned}\frac{\partial u}{\partial t}(x,t)&= -c \frac{\partial u}{\partial x}(x,t)+f(x,t) \\ u(x,0)&= g(x)\end{aligned}\]

です。\(f=0\)のときが同次移流方程式で、その解き方は既に紹介しました。移流方程式に\(f(x,t)\)という非同次項が加わった方程式です。

この方程式の解は、

\[ \begin{aligned}u(x,t)=g(x-ct)+\int_0^t f(x-c(t-s),s)ds\end{aligned} \]

と表せます。

この解は、波動方程式の解、ダランベールの公式を導出するために利用できます。

参考：1次元波動方程式の解：ダランベールの公式の証明、導出

では、非同次の移流方程式を解いてみましょう。

同次方程式の解は、\(u=g(x-ct)\)と表せるのでした。その仕組として、\((x,t)\)座標において、\((c,1)\)を通る直線は\((x+cs,t+s)\)と表せます。この直線上で解の値は一定です（\(x+cs-c(t+s)=x-ct\)）。同次の移流方程式の解は、その方向への微分が0として捉えられます。

そこで、\(v(s):= u(x+cs,t+s)\)と置いてみましょう。すると、その微分は、合成関数の微分から

\[ \begin{aligned} \frac{dv}{ds}&=c \frac{\partial u}{\partial x}(x+cs,t+s)+ \frac{\partial u}{\partial t}(x+cs,t+s)\\ &= f(x+cs,t+s) \end{aligned} \]

となります。これは積分によって解ける形です。両辺を\(-t\)から\(0\)まで積分すると、左辺は

\[ \begin{aligned} \int_{-t}^0 \frac{dv}{ds}ds &= z(0)-z(-t)\\ &=u(x,t)- u(x-ct,0)\\&= u(x,t)-g(x-ct)\end{aligned} \]

で、右辺は\(s\mapsto s-t\)の置き換えで、積分範囲が\(0\)から\(t\)に置き換わるので

\[ \begin{aligned} &\int_{-t}^{0} f(x+cs,t+s) ds \\&= \int _{0}^t f(x-c(t-s),s)ds\end{aligned} \]

となります。よって、

\[ \begin{aligned}u(x,t)=g(x-ct)+\int_0^t f(x-c(t-s),s)ds\end{aligned} \]

と解を得ることができました。

今回は\((x+cs,t+s)\)という直線に注目して問題を常微分方程式に落とし込みましたが、このような方法は一般に特性曲線法（method of characteristics）と呼ばれています。

以上、1次元の非同次の移流方程式の解き方を紹介してきました。紹介したのは1次元ですが、多次元でも全く同じ形の解が得られます。

波動方程式の理解の足がかりとしても、非同次の移流方程式に慣れてみてはいかがでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。