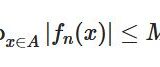1次元波動方程式の解き方：変数分離法、フーリエ級数展開

どうも、木村（@kimu3_slime）です。

今回は、1次元波動方程式の解き方、変数分離法、フーリエ級数を使った方法を紹介します。

波動方程式とは
変数分離法
フーリエ級数
こちらもおすすめ

波動方程式とは

\[ \begin{aligned}\frac{\partial^2 u}{\partial t^2} =c^2\frac{\partial^2 u}{\partial x^2}\end{aligned} \]

と表される偏微分方程式です。

参考：1次元の波動方程式（弦の振動）の導出：運動方程式から

今回は、有界領域\([0,L]\)において、端点が固定されている境界条件（ディリクレ境界条件）を考えましょう。

\[ \begin{aligned}u(0,t)=0,\quad u(L,t)=0\end{aligned} \]

また、初期条件を

\[ \begin{aligned}u(x,0)=f(x),\quad \frac{\partial u}{\partial t}(x,0)=g(x)\end{aligned} \]

とします。これらのすべてを満たす解、初期値・境界値問題の解を求めていきましょう。

主に

変数分離法によって、問題を2つの常微分方程式に帰着させる
境界条件から、常微分方程式の解を決定する
フーリエ級数を使って、初期条件を満たす解を2で得た解の重ね合わせとして構成する

というステップで議論します。

変数分離法

\[ \begin{aligned}u(x,t)= F(x)G(t)\end{aligned} \]

と空間\(x\)、時間\(t\)のみを変数とする関数にばらした解\(u\)を求める方法を、変数分離法（method of separating variables）と呼びます。

仮に上のように積に分解されたとして、解を求めてみましょう。

時間、空間2回微分はそれぞれ

\[ \begin{aligned}\frac{\partial^2 u}{\partial t^2} =F G^{\prime \prime}\end{aligned} \]

\[ \begin{aligned}\frac{\partial^2 u}{\partial x^2} =F^{\prime \prime} G\end{aligned} \]

なので、これを方程式に代入すると

\[ \begin{aligned}F G^{\prime \prime} = c^2 F^{\prime \prime} G\end{aligned} \]

となります。

ここで、\(u\)として自明な解\(u \equiv 0\)でないものを考えると、\(u=FG \neq 0\)となる点\(x_0,t_0\)が存在します。そこで両辺を\(c^2 FG\)で割ると、

\[ \begin{aligned}\frac{ G^{\prime \prime}}{c^2 G} (t_0)= \frac{F^{\prime \prime} }{F}(x_0)\end{aligned} \]

となります。これを\(\lambda\)と置きましょう。この\(\lambda \)は分離定数（separation constant）と呼ばれます。

これを使うと、一方の関数のみの方程式としてまとめられます。

\[ \begin{aligned}F^{\prime \prime }(x) =\frac{ G^{\prime \prime} (t_0)}{c^2 G(t_0)} F(x)=\lambda F(x)\end{aligned} \]

\[ \begin{aligned}G^{\prime \prime }(t) =\frac{ F^{\prime \prime} (x_0)}{ F(x_0)} c^2G(t)=\lambda c^2 G(t)\end{aligned} \]

こうして問題は、2つの常微分方程式を解くことに帰着されました。

これは関数\(F,G\)と2回微分に関する固有値問題となっています。

境界条件を使って、この2つの方程式の解を求めていきましょう。

\[ \begin{aligned}F(0)G(t) = 0, \quad F(L)G(t)=0\end{aligned} \]

ですが、\(G(t_0) \neq 0\)より\(F(0)=0\)、\(F(L)=0\)が得られます。

2階線形微分方程式は、\(\lambda\)の値によって次のように解くことができます。

\[ \begin{aligned} F(x) = \left\{ \begin{array}{l} C_1 e^{\sqrt{\lambda} x} + C_2 e^{\sqrt{-\lambda}x} & \lambda>0 \\ C_1 + C_2 x & \lambda =0 \\ C_1 \cos{\sqrt{-\lambda}x } + C_2 \sin {\sqrt{-\lambda}x } & \lambda <0 \end{array} \right. \end{aligned} \]

参考：同次形の2階線形微分方程式の解き方、学ぶ意味：熱方程式への応用を例に

ただし、\(\lambda \geq 0\)のときは、境界条件\(F(0)=F(L)=0\)から係数が\(C_1=C_2=0\)となります。

今求めたいのは自明解以外なので、\(\lambda < 0\)でなければなりません。境界条件から、

\[ \begin{aligned}C_1 =0\end{aligned} \]

\[ \begin{aligned}C_2 \sin {\sqrt{-\lambda}L} =0\end{aligned} \]

となりますが、\(C_2 =0\)とすると自明解になるので、\(C_2 \neq 0\)のケースを考えます。つまり、\(\sin {\sqrt{-\lambda}L} =0\)を解くと、\(n\)を整数として\( \sqrt{-\lambda}L=n\pi\)、\(\lambda_n =-(\frac{n\pi}{L})^2\)です。よって、

\[ \begin{aligned}F(x) =C_{2,n} \sin (\frac{n\pi}{L}x)\end{aligned} \]

という解が得られました。

\(G\)について、\(G^{\prime \prime }= \lambda _n c^2 G\)を解くと、

\[ \begin{aligned}G_n(t) = (A_n \cos \frac{cn\pi}{L}t +B_n \sin \lambda_n c t)\end{aligned} \]

となります（複素固有値、実部0）。

よって、変数分離法によって

\[ \begin{aligned}u_n(x,t)=(A_n \cos \frac{cn\pi}{L} t +B_n \sin \frac{cn\pi}{L}t) \sin (\frac{n\pi}{L}x)\end{aligned} \]

という解が得られました。

フーリエ級数

ここまでで、境界条件を満たす解が得られました。求めたいのは、さらに初期条件も満たす解です。そこで、

\[ \begin{aligned}u(x,t)= \sum _{n=1}^ \infty u_n(x,t)\end{aligned} \]

とこれまでの重ね合わせの解を考えましょう。波動方程式は線形方程式なので、解の重ね合わせもまた解となります。

参考：偏微分方程式とは：2階線形の重要な例（ラプラス、熱、波動）

初期条件\(u(x,0)=f(x) \)から、

\[ \begin{aligned}\sum_{n=1} ^\infty A_n \sin (\frac{n\pi}{L}x) = f(x)\end{aligned} \]

です。\(f\)はこのような三角級数（フーリエ級数）に展開できることが知られています。境界条件から、コサインの項が消え、サインのみが登場する展開（フーリエサイン級数）になっています。

両辺に\(\sin (\frac{k\pi}{L}x)\)をかけて積分すると、三角関数の積分の内積による直交性から、係数\(A_n\)は

\[ \begin{aligned}A_n = \frac{2}{L} \int _0 ^L f(x) \sin (\frac{n\pi}{L}x) dx\end{aligned} \]

と決定できます。

初期条件\(\frac{\partial u}{\partial t}(x,0)=g(x) \)について考えます。級数は一様収束していれば項別微分可能で、

\[ \begin{aligned}\frac{\partial u}{\partial t}(x,t) \\= \sum_{n} (-A_n \frac{cn\pi}{L}\sin \frac{cn\pi}{L} t +B_n \frac{cn\pi}{L}\cos \frac{cn\pi}{L}t) \sin (\frac{n\pi}{L}x) \end{aligned} \]

\[ \begin{aligned}\frac{\partial u}{\partial t}(x,0)\\= \sum_{n} B_n \frac{cn\pi}{L}\sin (\frac{n\pi}{L}x)\\ =g(x) \end{aligned} \]

となります。\(g\)についてもこのような展開（フーリエ級数展開）は可能です。さきほどと同様の議論で、係数は

\[ \begin{aligned} B_n &= \frac{2}{L \frac{cn\pi}{L}} \int _0^ L g(x) \sin (\frac{n\pi}{L}x) dx\\ &= \frac{2}{cn\pi} \int _0^ L g(x) \sin (\frac{n\pi}{L}x) dx\end{aligned} \]

と求められます。

以上によって、

\[ \begin{aligned}u(x,t)=\sum_{n=1}^\infty (A_n \cos \frac{cn\pi}{L} t +B_n \sin \frac{cn\pi}{L}t) \sin (\frac{n\pi}{L}x)\end{aligned} \]

が初期値・境界値問題の解であることがわかりました。（厳密に言えば、級数が一様収束し、項別微分可能であることを確かめる必要があります。）

参考：関数列の各点収束、一様収束とは、例と違い、求め方

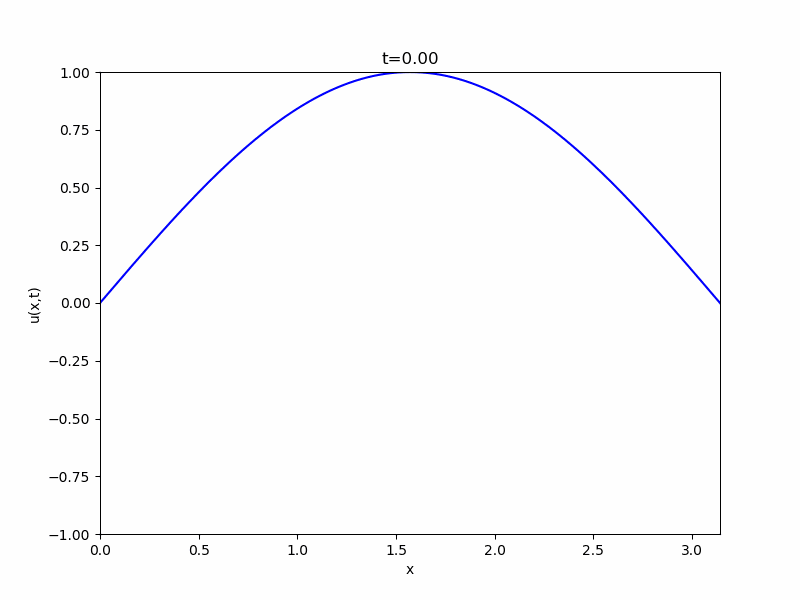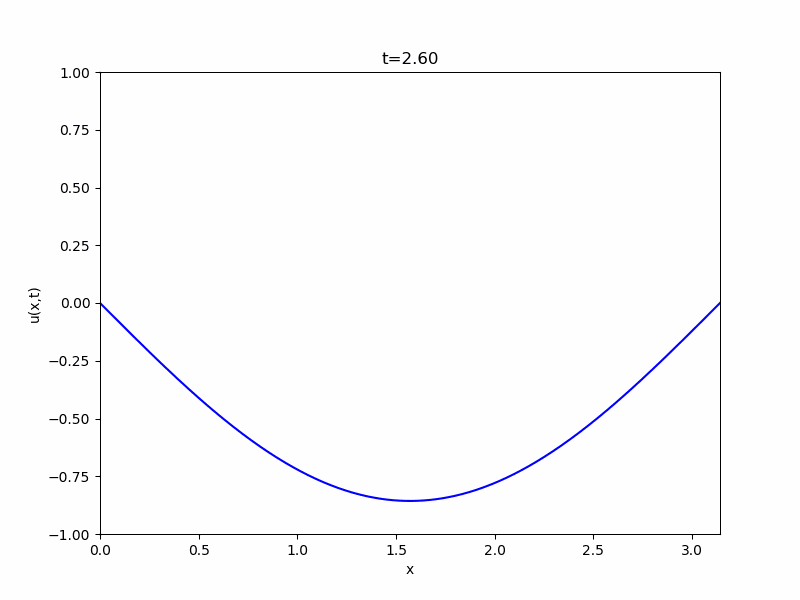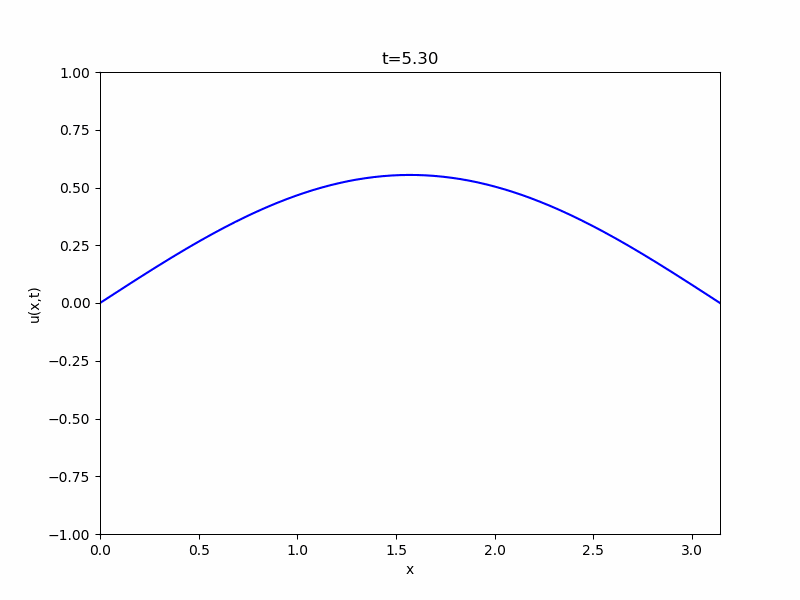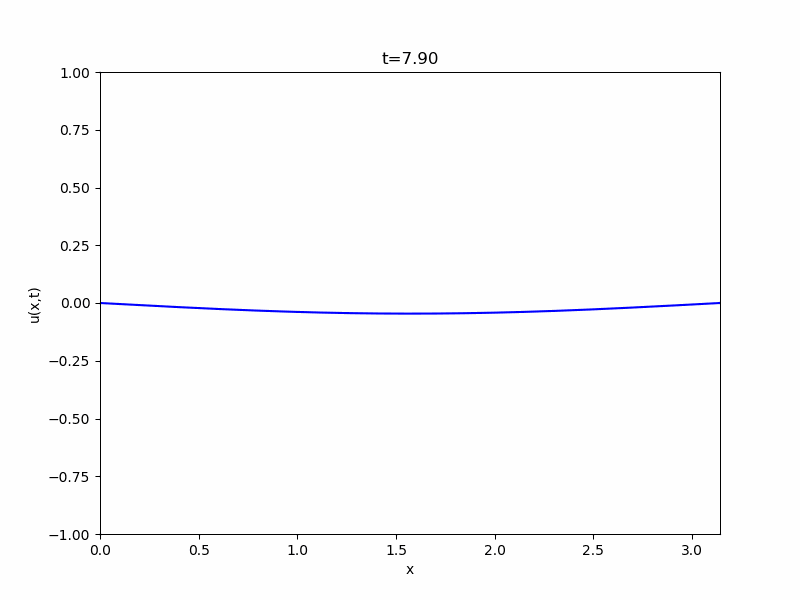
簡単な例として、\(L= \pi,c=1\)、\(u(x,0)= \sin x\)、\(\frac{\partial u}{\partial t}(x,0)=0\)という初期条件での解を考えてみましょう。

まず、係数は\(B_n=0\)となります。また、三角関数の直交性から\(A_1 = 1\)、\(A_n =0, n \geq 2\)です。よって、

\[ \begin{aligned}u= \cos t \sin x\end{aligned} \]

が解として得られました。