どうも、木村(@kimu3_slime)です。
今回は、弾性梁(はり)のたわみ曲線を、微分方程式を解いて求めてみます。
水平に置かれた直方体の金属、梁(はり beam)の変形について考えましょう。
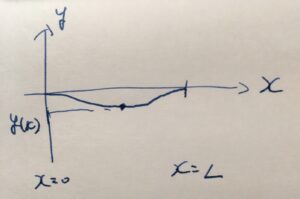
端点を\(x=0,L\)として、そこでは梁が固定されているとします。梁に何か重みがのったとすると、中間の点では荷重によって沈みこみ、何らかの曲線が生まれるでしょう。位置\(x\)における、梁のもとの高さとの変位を\(y(x)\)としましょう(下向きを正とする)。
梁のなす曲線\(y(x)\)は、たわみ曲線(deflection curve)、弾性曲線(elastic curve)と呼ばれるものです。
弾性体の理論、構造力学によると、次のような微分方程式を導くことができます。
梁の曲げモーメントを\(M(x)\)、梁に単位長さあたりにかかっている重さを\(f(x)\)とすると、
\[ \begin{aligned}\frac{d^2 M}{dx^2}(x)=f(x)\end{aligned} \]
が成り立ちます。今回は、一様な荷重を持つ\(f(x)= f_0\)としましょう(等分布荷重、等分布外力)。
また、曲げモーメントと梁の変位の間には、変位が小さいときは
\[ \begin{aligned}M(x)= EI\frac{d^2y}{dx^2}(x)\end{aligned} \]
という関係が成り立ちます。\(E,I\)は定数で、\(E\)は弾性体のヤング率、\(I\)は梁の断面の中心を通る水平な直線に関する慣性モーメントです。
まとめると、
\[ \begin{aligned} \frac{d^4 y}{dx^4} (x) = k\end{aligned} \]
\(k= \frac{f_0}{EI}\)という、4階の微分方程式が得られました。
この微分方程式を解いてみましょう。シンプルな形をしているので、積分を繰り返して解くことができます。
\[ \begin{aligned}\frac{d^3 y}{dx^3} = kx +C_1\end{aligned} \]
\[ \begin{aligned}\frac{d^2 y}{dx^2} = \frac{1}{2}kx^2 +C_1 x + C_2\end{aligned} \]
\[ \begin{aligned}\frac{d y}{dx} = \frac{1}{6}kx^3 +\frac{1}{2}C_1 x^2 + C_2 x + C_3\end{aligned} \]
\[ \begin{aligned}y = \frac{1}{24}kx^4 +\frac{1}{6}C_1 x^3\\ +\frac{1}{2} C_2 x^2 + C_3x +C_4\end{aligned} \]
と一般解を得ることができました。
端点\(x=0,L\)での梁の固定の仕方、境界条件(boundary condition)によって、たわみ曲線\(y(x)\)のようすは変わってきます。
単純に下から支えた場合(単純支持梁 simply supported beam)は
\[ \begin{aligned}y(0)=y(L)=0\end{aligned} \]
\[ \begin{aligned}\frac{d^2y}{dx}(0)=\frac{d^2y}{dx}(L)=0\end{aligned} \]
に対応します(2回微分=曲げモーメントが0)。このとき、2回微分の条件から
\[ \begin{aligned}C_2 =0\end{aligned} \]
\[ \begin{aligned}C_1 = -\frac{1}{2}kL\end{aligned} \]
で、端点での変位の条件から
\[ \begin{aligned}C_4 =0\end{aligned} \]
\[ \begin{aligned}C_3 =-\frac{1}{24}kL^3-\frac{1}{6}C_1 L^2\\ =\frac{1}{24} kL^3\end{aligned} \]
となるので、たわみ曲線は
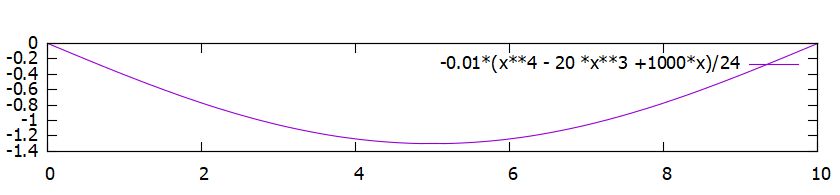
\[ \begin{aligned}y=\frac{1}{24}k(x^4-2Lx^3 + L^3 x) \end{aligned} \]
となりました。これは中点\(x= \frac{L}{2}\)について対称で、そこで最大値\(\frac{5}{24\cdot 16}kL^4\)を取ります。
別の境界条件として、端点を壁に埋め込んだ状態、固定端
\[ \begin{aligned}y(0)=y(L)=0\end{aligned} \]
\[ \begin{aligned}\frac{d y}{dx}(0)=\frac{dy}{dx}(L)=0\end{aligned} \]
の状況を考えましょう。このときは、
\[ \begin{aligned}C_3=0\end{aligned} \]
\[ \begin{aligned}\frac{1}{6}kL^2+\frac{1}{2}C_1L+C_2=0\end{aligned} \]
\[ \begin{aligned}C_4=0\end{aligned} \]
\[ \begin{aligned}\frac{1}{24}kL^2+\frac{1}{6}C_1L+\frac{1}{2}C_2=0\end{aligned} \]
\[ \begin{aligned}C_1 = -\frac{1}{2}kL\end{aligned} \]
\[ \begin{aligned}C_2 =\frac{1}{12} kL^2\end{aligned} \]
となるので、たわみ曲線は
\[ \begin{aligned}y(x) = \frac{1}{24}k(x^4-2Lx^3 +L^2x^2)\end{aligned} \]
となります。こちらも中点\(x= \frac{L}{2}\)について対称で、そこで最大値\(\frac{1}{24\cdot 16}kL^4\)を取ります。
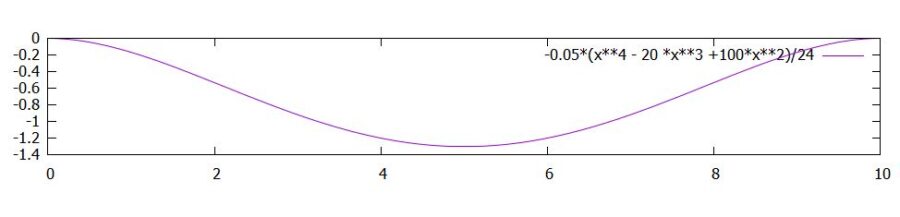
\(k\)が一定のときは、単純な支えと固定端の最大値を比較すると\(\frac{5}{24\cdot 16}kL^4>\frac{1}{24\cdot 16}kL^4 \)なので、固定端の方が変形の大きさが小さいことがわかりますね。
以上、梁の変形について、たわみ曲線・弾性曲線を微分方程式を解いて求めてみました。
一般には4階の微分方程式は複雑ですが、ごく単純な近似式を考えると、今回のように簡単な計算で解けて嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)