どうも、木村(@kimu3_slime)です。
今回は、非同次の2階線形微分方程式の解き方、未定係数法を、強制振動を例に紹介します。
非同次の2階線形微分方程式
\[ \begin{aligned}\frac{dx^2}{dt^2}+a \frac{dx}{dt}+bx = R(t)\end{aligned} \]
という形の2階線形微分方程式を考えましょう。\(a,b\)は定数です。
\(R(t)=0\)のときは同次(斉次 homogeneous)方程式、\(R(t) \neq 0\)のときは非同次(非斉次 nonhomogeneous)と呼びます。
非同次方程式の一般解(general solution)は、同次方程式の解\(x_h(t)\)と非同次方程式のひとつの解(特殊解 particular solution)\(x_p (t)\)の和として求めることができます。
\[ \begin{aligned}x(t)= x_h (t)+x_p(t)\end{aligned} \]
実際、何らかの方法で特殊解\(x_p\)を見つけられたとしましょう。\(x\)を一般解として、\(y =x – x_p\)を非同次の方程式に代入します。すると、
\[ \begin{aligned} & \frac{dy^2}{dt^2}+a \frac{dy}{dt}+by \\&\frac{d^2}{dt^2}(x-x_p)+ a \frac{d}{dt}(x-x_p)+b(x-x_p)\\&=\frac{dx^2}{dt^2}+a \frac{dx}{dt}+bx \\&-(\frac{dx_p^2}{dt^2}+a \frac{dx_p}{dt}+bx_p ) \\ &= R(t)-R(t) \\ &= 0\end{aligned} \]
となって、\(y\)に関する同次方程式が得られました。
同次方程式の解き方は、既に知られているので、\(y=x_h\)を得ることができます。
参考:2階線形常微分方程式の解き方、学ぶ意味:熱方程式への応用を例に、線形微分方程式はなぜ指数関数e^{λt}と仮定して解いて良いか
よって、\(x= x_h+x_p\)が得られました。
つまり、非同次の線形微分方程式を解く問題は、特殊解\(x_p\)を求める問題に帰着されます。
簡単な例では、多項式関数、指数関数、三角関数などを使うことで、特殊解を見つけることができるでしょう。特殊解の形を想定して係数を決めることによって特殊解を求める方法は、未定係数法(method of undetermined coefficients)と呼ばれるものです。
より一般には、微分演算子を使った方法、定数変化法が必要となります。
強制振動の方程式
非同次の方程式の例として、今回は、\(R(t) = F \cos \omega t\)、\(\omega >0\)
\[ \begin{aligned}\frac{dx^2}{dt^2}+\omega _0 ^2 x = F \cos \omega t\end{aligned} \]
という微分方程式を考えましょう。これはおもりばね系に周期的な外力\(R(t)\)が加わった方程式で、強制振動(forced oscillation)の方程式と呼ばれます。
うなり
非同次方程式を解くために、特殊解を探したいです。
非同次項はコサインなので、コサインを使って特殊解を見つけられないでしょうか。すなわち、\(A \cos \omega t\)を方程式に代入し、\(A\)を求められないか試してみましょう(未定係数法)。
\[ \begin{aligned}-A \omega ^2 \cos \omega t + A \omega _0 ^2\cos \omega t= F \cos \omega t\end{aligned} \]
となるので、
\[ \begin{aligned}A = \frac{F}{ \omega_0^2 -\omega ^2}\end{aligned} \]
と置けば、
\[ \begin{aligned}x_p(t) = \frac{F}{ \omega_0 ^2 -\omega ^2} \cos \omega t\end{aligned} \]
は特殊解です。この議論をするためには、\(\omega_0 \neq \omega\)である必要がありますね。
同次形の方程式の解は、すでにおもりバネ形で見たように、
\[ \begin{aligned}x_h(t) = C_1 \cos \omega_0 t +C_2 \sin \omega_0 t\end{aligned} \]
となります。よって、一般解は
\[ \begin{aligned}x(t) =C_1 \cos \omega_0 t +C_2 \sin \omega_0 t\\+ \frac{F}{ \omega_0 ^2 -\omega ^2} \cos \omega t \end{aligned} \]
と求めることができました。
これは2つの各周波数\(\omega ,\omega _0\)の振動を、重ね合わせた振動となっています。

特に、\(\omega_0 ,\omega\)が近い値のときは、速い振動と遅い振動が合わさった現象が見られます。これはうなり(beats)と呼ばれるものです。
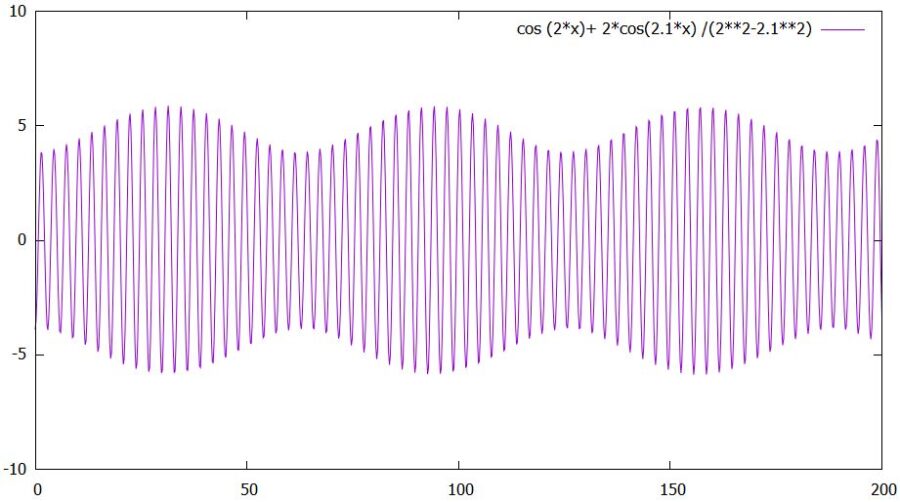
共鳴
\(\omega = \omega_0\)のときは、特殊解をどうやって見つけたら良いでしょうか。
さきほど使った\(A \cos \omega_0 t\)は、同次方程式の解となっているので、非同次方程式の解となりません。そんなときは、\(t\)をかけて
\[ \begin{aligned}x_p(t) = t (A \cos \omega_0 t +B \sin \omega _0 t)\end{aligned} \]
という形の特殊解が見つけられることが知られています(未定係数法)。これを代入して、係数を求めてみましょう。
\[ \begin{aligned}\frac{dx}{dt} = (A \cos \omega_0 t + B \sin \omega_0 t)\\+\omega_0 t (-A \sin \omega_0 t + B \cos \omega_0 t)\end{aligned} \]
\[ \begin{aligned}\frac{d^2x}{dt^2} = \omega_0 (-A \sin \omega_0 t + B \cos \omega_0 t)\\+\omega_0 (-A \sin \omega_0 t + B \cos \omega_0 t) \\ +\omega_0 ^2 t(-A \cos \omega_0 t -B \cos \omega _0 t) \\ = 2\omega_0 (-A \sin \omega_0 t + B \cos \omega_0 t) – \omega_0^2 x_p\end{aligned} \]
なので、方程式に代入すれば
\[ \begin{aligned}2\omega_0 (-A \sin \omega_0 t + B \cos \omega_0 t) \\ = F \cos \omega_0 t \end{aligned} \]
が得られます。これを常に成り立たせるためには、\(A=0\)、\(B = \frac{F}{2 \omega_0}\)とすれば良いですね。
よって、特殊解は
\[ \begin{aligned}x_p(t) =\frac{F}{2 \omega_0} t \sin \omega_0 t \end{aligned} \]
で、一般解は
\[ \begin{aligned}x(t) =C_1 \cos \omega_0 t +C_2 \sin \omega_0 t\\+\frac{F}{2 \omega_0} t \sin \omega_0 t \end{aligned} \]
と求めることができました。
\(t \sin \omega t\)の大きさは、時間が経つにつれ大きくなっていきます。すなわち、振幅がどんどん大きくなる現象が起こり、これは共鳴(resonance)と呼ばれるものです。
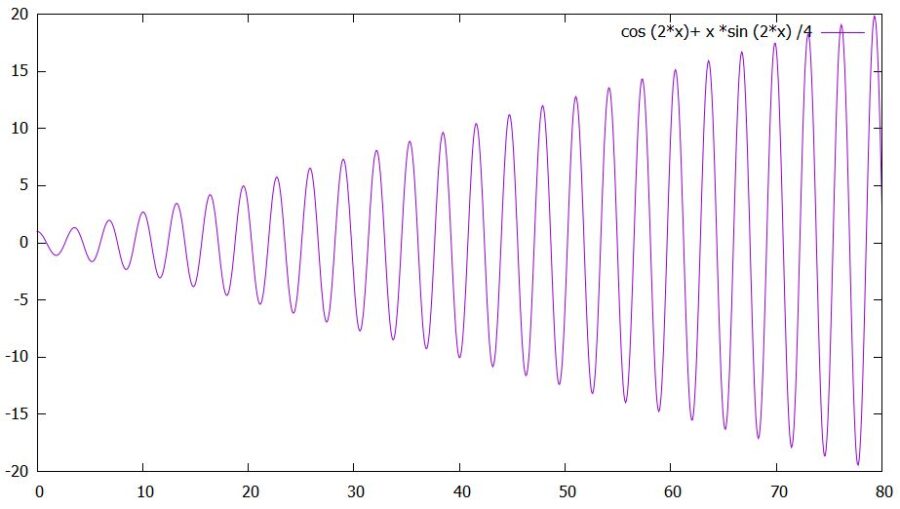
現実的には、際限なく振幅が大きくなることはないでしょう。ばねによる振動だけでなく、何らかの減衰(ダンパ)が加わるので。いずれにせよ、\(\omega = \omega_0\)のときは振幅は大きくなり、それも共鳴と呼ばれています。
以上、非同次の2階線形微分方程式の解き方、未定係数法を、強制振動を例に紹介してきました。
非同次の方程式の特殊解さえ見つけられれば、それを同次形の方程式の解と合わせることで一般解を得ることができます。適切に特殊解を予想して方程式に代入することによって、特殊解を見つけてみましょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
2階線形常微分方程式の解き方、学ぶ意味:熱方程式への応用を例に
線形微分方程式はなぜ指数関数e^{λt}と仮定して解いて良いか