RL直列回路の微分方程式の立て方、電流の求め方、過渡現象

どうも、木村（@kimu3_slime）です。

今回は、RL直列回路（抵抗コイル回路）の電流を、微分方程式を解いて求めてみます。

考えるのは、次のような電気回路です。

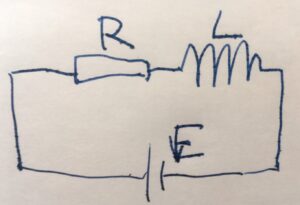
電圧\(E\)の電池、抵抗\(R\)の抵抗、インダクタンス\(L\)のコイルがあります。抵抗とコイルが直列につながれているので、これをRL直列回路と呼びます。

この図から、電流\(I(t)\)に関する微分方程式（回路方程式）を立ててみましょう。

まず電圧に注目しましょう。オームの法則より、抵抗によって\(E_R:=RI\)だけ電圧が下がります。コイルを流れる電流に依存して、\(E_L:=L\frac{dI}{dt}\)だけ電圧が下がります（誘導起電力、インダクタンスの定義）。

そして、キルヒホッフの第2法則「閉回路について、起電力の和と電圧降下の和は等しい」を適用しましょう。

\[ \begin{aligned}E_R+ E_L =E\end{aligned} \]

\[ \begin{aligned} RI+ L \frac{dI}{dt}=E\end{aligned} \]

です。\(I\)について整理すると、

\[ \begin{aligned}\frac{dI}{dt}+\frac{R}{L}I =\frac{E}{L}\end{aligned} \]

という微分方程式が得られました。

この方程式は、線形微分方程式として解くことができます。

まず、同次形の方程式

\[ \begin{aligned}\frac{dI}{dt}+\frac{R}{L}I =0\end{aligned} \]

は、変数分離形として、積分によって解くことができます。

\[ \begin{aligned} \int \frac{1}{I} dI= \int -\frac{R}{L} dt\end{aligned} \]

\[ \begin{aligned} \log |I|= -\frac{R}{L}t+C\end{aligned} \]

\[ \begin{aligned}I_1 (t)= C e^{-\frac{R}{L} t}\end{aligned} \]

です。定数変化法として、\(I (t) =C(t)e^{-\frac{R}{L} t}\)を非同次の方程式に代入しましょう。

\[ \begin{aligned}\frac{dC}{dt}e^{-\frac{R}{L} t}-\frac{R}{L}Ce^{-\frac{R}{L} t}+\frac{R}{L}Ce^{-\frac{R}{L} t}=\frac{E}{L}\end{aligned} \]

\[ \begin{aligned}\frac{dC}{dt}=\frac{E}{L}e^{\frac{R}{L} t}\end{aligned} \]

これを積分すると、

\[ \begin{aligned}C(t) = \frac{E}{R} e^{\frac{R}{L} t} +C\end{aligned} \]

となります。これを使えば、

\[ \begin{aligned} I(t)&=C(t)e^{-\frac{R}{L} t} \\&= \frac{E}{R} +Ce^{-\frac{R}{L} t} \end{aligned} \]

と解が求められました。初期条件を\(I(0)=I_0\)とすると、

\[ \begin{aligned}I(t)=\frac{E}{R} +(I_0 -\frac{E}{R})e^{-\frac{R}{L} t}\end{aligned} \]

となります。

この解は、指数関数の効果によって、\(t\)が大きくなると一定の値に近づきます。すなわち、\(\lim_{t \to \infty} I(t) = \frac{E}{R}\)です。

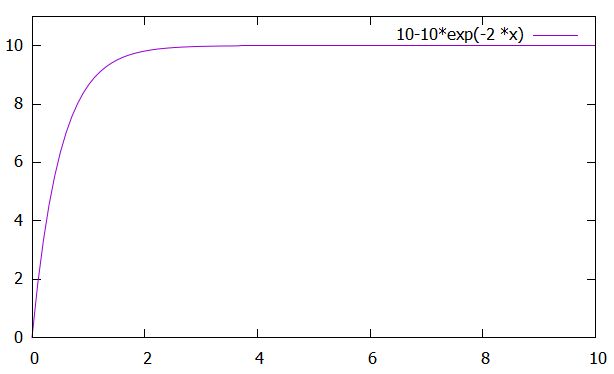
この回路にスイッチをつけ、\(I_0=0\)から電流を流し始めたとしましょう。最初はコイルによって電圧増加が妨げられるわけですが、抵抗と電源の電圧と合わさって、つりあいの状態に向かっていきます。つまり、電流は一定（\(\frac{R}{E}\)）になります。

電流が一定になった状態は定常状態（steady state）、定常状態に向かうまでの変化している状態を過渡状態（transient state）、非定常状態と呼びます。全体を通し、過渡状態から定常状態へ変化するような現象は、過渡現象（transient phenomena）と呼ばれるものです。

定常状態は、次のように求めることもできます。変化がない\(\frac{dI}{dt}=0\)ので、\(\frac{R}{L}I =\frac{E}{L}\)となり、\(I= \frac{E}{R}\)と。

高校物理でもRL回路について学ぶでしょうが、微分方程式を解くと、その理屈に納得しやすいと思います。

参考：5分でわかる！ＲＬ回路 – Tryit

以上、RL回路の微分方程式の立て方、電流の求め方を紹介してきました。

コンデンサを含んだRLC回路を考えるためにも、まずはRL回路を基礎として知っておくと良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。