どうも、木村(@kimu3_slime)です。
\(\sum_{n=1}^{\infty} \frac{1}{\sqrt{n}}\)、\(\sum_{n=1}^{\infty} \frac{1}{n}\)、\(\sum_{n=1}^{\infty} \frac{1}{n^2}\)、\(\sum_{n=1}^{\infty} \frac{1}{n^3}\)のような無限級数は、収束するでしょうか、発散するでしょうか。
今回は、負のべき乗の無限級数\(\sum_{n=1}^{\infty} \frac{1}{n^p}\)の収束・発散の判定方法を紹介します。
級数の収束・発散を判定するために、関数\(f(x)= \frac{1}{x^p}\)との比較をしましょう。\(p>0\)は実数としています。
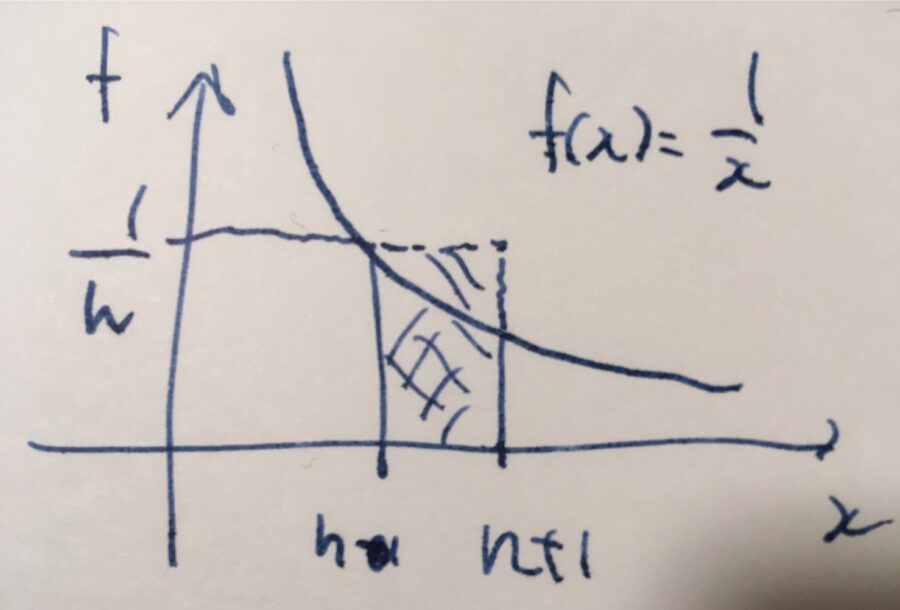
\(n\)を任意の自然数とします。このとき、面積の比較(積分の単調性)から、
\[ \begin{aligned}\frac{1}{(n+1)^p} \leq \int_{n}^{n+1}\frac{1}{x^p}dx \leq \frac{1}{n^p}\end{aligned} \]
が成り立ちます。\(n=1\)から\(n=k\)までの和を取り、左辺を整理すると
\[ \begin{aligned}\sum_{n=1}^{k+1}\frac{1}{n^p} -1 \leq \int_{1}^{k+1}\frac{1}{x^p}dx \leq\sum_{n=1}^k \frac{1}{n^p}\end{aligned} \]
となり、\(k\to \infty\)の極限を取れば
\[ \begin{aligned}\sum_{n=1}^{\infty}\frac{1}{n^p} -1 \leq \int_{1}^{\infty}\frac{1}{x^p}dx \leq\sum_{n=1}^\infty \frac{1}{n^p}\end{aligned} \]
となりました。
したがって、負のべき乗の広義積分を評価すれば良い、ということになります。それは
\[ \begin{aligned} \int_{1}^{\infty}\frac{1}{x^p}dx = \begin{cases}\infty & (0 <p \leq 1 )\\ \frac{1}{p-1}& (p>1)\end{cases}\end{aligned} \]
と計算できます。
よって、\(0<p\leq 1\)のとき、
\[ \begin{aligned} \int_{1}^{\infty}\frac{1}{x^p}dx \geq\sum_{n=1}^\infty \frac{1}{n^p} = \infty\end{aligned} \]
と発散し、\(p>1\)のときは
\[ \begin{aligned}\sum_{n=1}^{\infty}\frac{1}{n^p} \leq 1+\int_{1}^{\infty}\frac{1}{x^p}dx \leq 1+\frac{1}{p-1}\end{aligned} \]
と収束することがわかりました。
\(p=1\)のときは、\(\sum_{n=1}^\infty \frac{1}{n}\)は発散します。これは調和級数と呼ばれるものです。
\(p=2\)のとき、収束するだけでなく、その値が
\[ \begin{aligned}\sum_{n=1}^\infty \frac{1}{n^2}= \frac{\pi^2}{6}\end{aligned} \]
であることが知られています。これはバーゼル問題という名前がついている問題です。いくつかの証明方法が知られていますが、例えばフーリエ級数展開・パーセバルの等式から導けることが知られています。
また、べきの部分を変数として捉えた関数
\[ \begin{aligned}\zeta (s):= \sum_{n=1}^\infty \frac{1}{n^{s}}\end{aligned} \]
はリーマンのゼータ関数と呼ばれます。右辺はゼータ級数と呼ばれることも。
どんな値を取るかはわかりませんが、少なくとも\(s>1\)の実数に対し、右辺の級数が収束することは示せました。
複素解析における解析接続という考え方を用いることで、\(s\)は実数に限らず複素数について定義された関数として捉えられます。この関数は素数の分布と関係していて、それに関する未解決の予想はリーマン予想と呼ばれています。
以上、負のべき乗の無限級数\(\sum_{n=1}^{\infty} \frac{1}{n^p}\)の収束・発散の判定方法を紹介してきました。
同じ形の広義積分の収束発散と同様に、\(p>1\)かどうかで収束か発散かが分かれます。この結果を知っていれば、より一般の級数が収束・発散するかどうかについて、比較対象として利用できますね。
収束したときの値がどうなるかはともかく、収束・発散の判定をするのは難しくないので、基本的な結果として利用してみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版 (1984-12-21T00:00:01Z)
¥682 (中古品)
岩波書店 (1978-03-23T00:00:01Z)
¥5,060
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080
東京大学出版会 (1985-04-25T00:00:01Z)
¥1,884 (中古品)