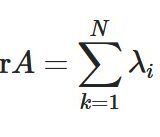2次形式の標準形、符号、シルベスターの慣性法則とは

どうも、木村（@kimu3_slime）です。

今回は2次形式に標準形、符号、シルベスターの慣性法則とは何か、具体例を交えて紹介します。

標準形、符号、シルベスターの慣性法則
ラグランジュの方法
こちらもおすすめ

標準形、符号、シルベスターの慣性法則

\(f(x_1,x_2)=ax_1^2+2bx_1x_2+cx_2^2\)のように、2次の項のみからなる多変数の多項式を2次形式と言いました。

2次形式は、対称行列\(A\)を使って一般に

\[ \begin{aligned}f(x) =x^\top Ax= \langle x ,Ax\rangle\end{aligned} \]

と表されます。この2次形式のできるだけ簡単な形を提示するのが、シルベスターの慣性法則です。

\(A\)は対称行列なので、必ず対角化できます。またすべての固有値は実数となります。

シルベスターの慣性法則では、固有値が正か負か0であるかに注目します。\(A\)の正の固有値を\(p\)個\(\lambda_1,\dots,\lambda_p\)、負の固有値を\(q\)個\(\lambda_{p+1},\dots,\lambda_{p+q}\)個としましょう。残りは0固有値です。この順に固有値を並べて対角化しましょう。

\(P\)を直交行列として、\(Ax=PD P^{-1}x\)において、\(y=P^{-1}x\)とおけば、

\[ \begin{aligned} f(x) &= x^\top Ax \\&=y^\top P^\top PDP^{-1}x\\&= y^\top D y \\&=\lambda_1 y_1^2+\cdots+\lambda_p y_p ^2 \\&+ \lambda_{p+1} y_{p+1}^2+\cdots+\lambda_{p+q}y_{p+q}^2 \end{aligned} \]

となります。

さらに変数変換\(z_1 = \sqrt{\lambda_1}y_1,\dots,z_p =\sqrt{\lambda_p}y_p\)、\(z_{p+1} = \sqrt{-\lambda_1}y_{p+1},\dots,z_{p+q} =\sqrt{-\lambda_{p+q}}y_{p+q}\)をすると、

\[ \begin{aligned} f(x)&= z_1^2+\cdots+ z_p ^2 \\&- z_{p+1}^2-\cdots-z_{p+q}^2\end{aligned} \]

と表されます。

これを2次形式の標準形と呼びます。また、正負の項の数を表す\((p,q)\)を2次形式の符号と呼びます。（差\(p-q\)を符号ということもある）

例えば、

\[ \begin{aligned}A=\begin{pmatrix} 0 &1\\1 & 0 \end{pmatrix}\end{aligned} \]

により定まる2次形式の標準形と符号を求めてみましょう。対角化の計算は省略しますが、固有値は\(1,-1\)で、\(y=P^{-1}x\)と置くと

\[ \begin{aligned}f(x)=y_1^2 -y_2^2\end{aligned} \]

と表されます。一般には固有値は1ではないので、ここから係数が1となるように変数変換する必要がありますが、今回は必要ありません。

よって、これが標準形で、符号は\((1,1)\)であるとわかりました。

さらに、次のような結果が成り立ちます。

シルベスターの慣性法則（Sylvester’s law of inertia）

\(A\)を対称行列とし、それにより定まる2次形式を考える。

2次形式には標準形が存在し、それは可逆な変数変換の仕方によらず一意的に定まる。

つまり、どんな可逆な変数変換をしても、符号\((p,q)\)は一定である。

証明は齋藤「線型代数入門」5章を参照してください。

行列\(A\)の正の固有値の個数\(p\)は正の慣性指数（positive index of inertia）、負の固有値の個数\(q\)は負の慣性指数（negative index of inertia）とも呼ばれます。慣性法則と呼ぶのは、見かけの形は変わっても残り続ける量（正負の固有値の個数）がある、という主張だからでしょう。

2次形式が正定値行列などであることに関しては、固有値の符号によって判定することができました。これを2次形式の符号の言葉で言えば、次のように表せます。

行列\(A\)のサイズを\(N\)とする。