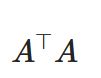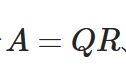どうも、木村(@kimu3_slime)です。
今回は、線形代数の立場から、最小二乗法とは何か、最小二乗解の求め方、射影による理解を紹介します。
最小二乗法とは
あるアサガオの成長記録から、成長を予測するモデルを考えたいとしましょう。つるの長さを記録して、次のデータがあったとします。(架空のデータです)
| 観測した記録 | |
| 日数 | 長さ |
| 3 | 5 |
| 6 | 11 |
| 9 | 16 |
| 12 | 20 |
およそ日数\(x\)と長さ\(y\)は比例関係にあるように見えるので、\(y=ax +b\)と直線で表せないか考えます。
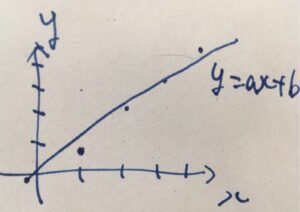
図で表したような直線を求めたいのですが、求めるべき\(a,b\)はどのようにして決めたら良いのでしょうか。
仮に\(y=ax+b\)という直線の上に、4つのデータ\((3,5),(6,11),(9,16),(12,20)\)があるとしましょう。すると、4つの連立方程式が得られます。
\[ \begin{aligned}3a+b=5,\quad 6a+b=11\end{aligned} \]
\[ \begin{aligned}9a+b=16,\quad 12a+b=20\end{aligned} \]
これを行列の言葉を使って表せば、
\[ \begin{aligned} \begin{pmatrix} 3 &1\\6 &1\\9 &1\\12 &1 \end{pmatrix}\begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} 5\\11\\ 16\\20 \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}Ax = c\end{aligned} \]
となります(\(x=(a,b)\)とした。\(y=ax+b\)の\(x\)とは別物なので注意)。
この連立線形方程式は、未知数2に対して方程式の本数が過剰であり、解を持ちません。(係数行列のランク2と拡大係数行列のランク3が一致しない)
参考:線形方程式の解き方:ガウスの消去法と基本変形・ランク、LU分解
つまり、1本の直線で元のデータを完全に再現することはできません。しかし、それでもできるだけデータをよく近似するような直線を求めたい。そこで登場するのが、最小二乗法という手法です。
\(Ax=c\)には解が存在しません。つまり、\(e:= \| Ax-c\|\)は0にはなりません。この\(e\)を残差二乗和(residual sum of squares)と呼びます。それが0にならなくても、できるだけ\(e\)が小さくなるような解\(x\)を求めたい。それを最小二乗解(least squares solution)、ノルム最小解(minimum norm solution)と呼びます。以降で紹介するように、実際に最小二乗解は必ず見つけられます。
なぜ二乗かというと、\(\|x\|= \sqrt{x_1^2+\cdots+ x_n ^2}\)という2乗和の(ユークリッド)ノルムで誤差を測っているからです。
最小二乗解は、次のような手順で見つけることができます。
\(Ax=c\)の両辺に転置行列\(A^\top \)をかけると、
\[ \begin{aligned}A^\top Ax =A^\top c\end{aligned} \]
という方程式が得られます。非正方行列であった\(A\)を正方行列の問題に変えたもので、これを正規方程式(normal equation)と呼びます。
左辺の行列\(A^\top A\)は\(A\)のグラム行列と呼ばれ、必ず正方行列・対称行列になり、\(A\)の列ベクトルが線形独立なとき可逆な行列となります。
実は、正規方程式の解が最小二乗解となります。とりあえず、さきほどの例で実際にやってみましょう。
正規方程式は
\[ \begin{aligned} \begin{pmatrix} 270 &30\\30 & 4 \end{pmatrix} \begin{pmatrix} a\\b \end{pmatrix}= \begin{pmatrix} 465\\ 52\end{pmatrix} \end{aligned} \]
となります。拡大係数行列を基本変形すると、
\[ \begin{aligned} &\begin{pmatrix} 270 &30 &465\\30 & 4 &52\end{pmatrix} \\ & \sim\begin{pmatrix} 270 &30 &465\\270 & 36 &468\end{pmatrix} \\ & \sim\begin{pmatrix} 270 &30 &465\\0 & 6 &3\end{pmatrix} \end{aligned} \]
となるので、\((a,b)= (\frac{5}{3} ,\frac{1}{2})\)が解として求められます。
\(y= \frac{5}{3}x + \frac{1}{2}\)がデータを精度良く近似するモデルというわけです。残差の2乗和は、計算してみると
\[ \begin{aligned} &\|Ax -c\|\\&= \sqrt{ (5+\frac{1}{2}-5)^2+(10+\frac{1}{2}-11)^2\\+(15+\frac{1}{2} -16)^2+(20+\frac{1}{2} -20)^2 }\\&=1 \end{aligned} \]
であるとわかります。
比較として、例えば\((a,b)=(\frac{5}{3},0)\)という直線を考えると、残差は\(\sqrt{2}\)となり、こちらの方が精度が悪いですね。
最小二乗法の原理:射影による理解
さて、なぜ正規方程式\(A^\top Ax =A^\top c\)を解くことで、最小二乗解が得られるのでしょうか。それは射影によって理解できます。
まず、状況を図に書いて幾何学的に理解しましょう。\(x\)がさまざまに動くとき、\(A\)による像\(Ax\)は平面となります(行列のランク=像の次元が2なので)。また、ベクトル\(c\)は、\(Ax =c\)に解がないので、平面上にないベクトルになります。
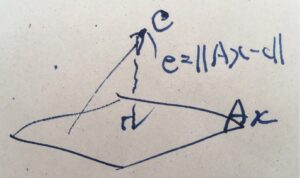
探したいのは、\(e= \|Ax -c\|\)を最小にする\(x\)です。そのような\(x\)は、\(c\)の平面(\(A(\mathbb{R}^2)\))への直交射影となります。斜めになるような点を選んだら、直交射影に比べて距離が大きくなりますね。
正規方程式の解\(\hat{x}=(A^\top A)^{-1}A^\top c\)の像\(A\hat {x}\)は、\(c\)の\(A(\mathbb{R}^2)\)への直交射影となっていることを確かめてみましょう。
\(A\hat{x} =A(A^\top A)^{-1}A^\top c\)なので、\(P=A(A^\top A)^{-1}A^\top\)と置きます。すると、
\[ \begin{aligned} P^2 &=A(A^\top A)^{-1}A^\top A(A^\top A)^{-1}A^\top \\ &= A(A^\top A)^{-1}A^\top A A^{-1}(A^\top) ^{-1}A^\top \\ &=A(A^\top A)^{-1}A^\top \\ &= P\end{aligned} \]
\[ \begin{aligned} P^{\top} &= (A^\top)^\top ((A^\top A)^{-1} )^\top A^\top \\&= A ((A^\top A)^\top )^{-1} A^\top \\&= A(A^\top A)^{-1}A^\top \\ &= P\end{aligned} \]
なので、\(P\)は直交射影行列です。つまり、\(A\hat {x} = Pc\)は\(c\)の\(A(\mathbb{R}^2)\)への直交射影となります。
正規方程式の解を見つけるということは、\(c\)の\(A\)の像への直交射影を見つけることだった、というわけです。確かに、そのような解は誤差を最小化しそうです。
\(Ax-c\)というベクトルを、\(A\)の像とそれに直交する成分に分けると、
\[ \begin{aligned}Ax -c = Ax- A\hat{x} +A\hat {x} -c\end{aligned} \]
となり、直交しているのでノルムについて三平方の定理が成り立ち、
\[ \begin{aligned}\|Ax-c\|^2 =\|Ax- A\hat{x}\|^2 +\|A\hat {x}-c\|^2\end{aligned} \]
が得られます。
ここで\(x=\hat{x}\)(正規方程式の解)とすれば、\(\|Ax- A\hat{x}\|^2=0\)です。また、すべての\(y \neq \hat{x}\)に対して、\(\|A\hat {x}-c\|^2<\|Ay-c\|^2\)となります。つまり、\(x= \hat{x}\)が残差平方和\(e=\|Ax-c\|\)を最も小さくする最小化点(minimizer)です。
直交射影\(Pc\)は、元のベクトル\(c\)を最もよく近似する\(A\)の像上のベクトルで、これは直交射影の性質によるものです。
詳しくは:射影行列、射影作用素とは:例、定義、性質
以上、最小二乗法とは何か、最小二乗解の求め方としての正規方程式、原理としての射影について紹介してきました。
線形代数を使うと、最小二乗法を幾何学的・代数的に理解することができます。今回は紹介しませんでしたが、\(\|Ax-c\|^2\)を偏微分して最小化点を見つけることもできます。
具体例ではデータは\(5\)個で\(5,2\)行列を考えましたが、データが\(m\)個なら\(m,2\)行列を考えて同じことができます。
複数のデータを最もよく近似する直線を見つけたいときは、ぜひ最小二乗法を試してみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版 (1982-07-09T00:00:01Z)
¥788 (中古品)
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社 (2015-12-22T00:00:01Z)
¥14,721 (コレクター商品)
東京大学出版会 (2019-03-08T00:00:00.000Z)
¥1,870