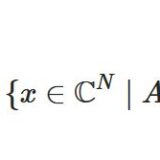不変部分空間とは：固有空間、射影行列を例に

どうも、木村（@kimu3_slime）です。

今回は、不変部分空間とは何か、固有空間、射影を例に紹介します。

不変部分空間とは
- 固有空間
- 射影行列
こちらもおすすめ

不変部分空間とは

\(A\)を\(N\)次の正方行列、\(W\)を\(\mathbb{R}^N\)の部分空間とします。

\(W\)が\(A\)について不変部分空間（invariant subspace）であるとは、\(A(W) \subset W\)が成り立つことです。\(W\)は\(A\)-不変であるとも。

左辺は\(A\)による\(W\)の像で、

\[ \begin{aligned}A(W):= \{ y \in \mathbb{R}^ N \mid y=Ax となる x \in W が存在する\}\end{aligned} \]

のことでした。

\(W\)全体を線形変換\(A\)によって写しても、\(W\)をはみ出るようなことがない、それが不変部分空間であるということです。

固有空間

不変部分空間の例としては、固有空間があります。

行列\(A\)と数\(\lambda \)に対し、

\[ \begin{aligned}E(\lambda)= \{ x \mid Ax = \lambda x\}\end{aligned} \]

により定まる部分空間を、固有空間というのでした。

固有空間\(E(\lambda)\)が、行列\(A\)について不変であることを確かめましょう。つまり、\(A(E(\lambda)) \subset E (\lambda)\)を示せば良いです。

任意に\(y \in A(E(\lambda))\)を選ぶと、像の定義から\(y= Ax\)、\(x \in E(\lambda)\)と表せます。\(x\in E(\lambda)\)より、\(Ax = \lambda x\)です。したがって、\(Ay = A(\lambda x) = \lambda Ax =\lambda y\)を満たします。よって、\(y \in E(\lambda)\)が言えました。

この証明と同様にして、ある固有ベクトルが生成する部分空間は、不変部分空間であると言えます。

そもそも、不変部分空間という概念は、固有空間が持つ性質を一般化したものと言えるでしょう。固有ベクトルを考えることは、その行列による変換が簡単になるベクトルを見つけることです。

\(\{0\}\)という1点集合（0次元線形空間）を考えると、それは任意の行列\(A\)の不変部分空間です。なぜなら、必ず\(A0 =0\)なので。このとき、\(x=0\)は\(A\)の不動点（fixed point）といったりします。

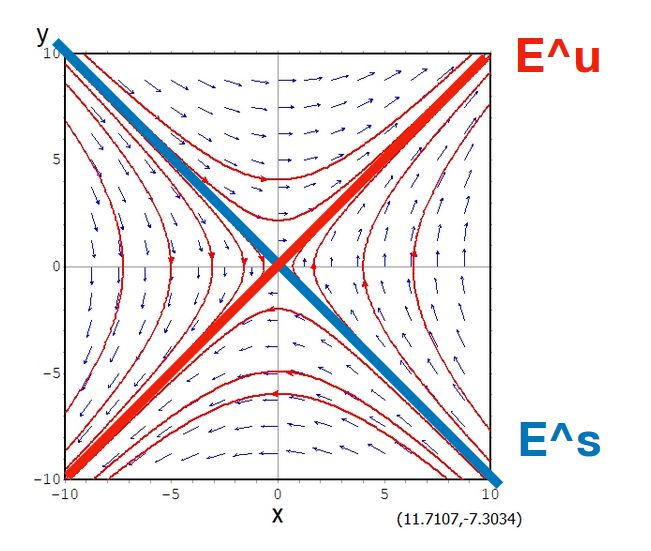
微分方程式の解の時間変化を調べる力学系の分野では、もっと一般に不変集合という概念を考えます。線形方程式では不変部分空間が見つかりますが、一般には（線形でない）不変部分集合が見つかるわけです。

参考：不変集合、安定・不安定・中心多様体とは何か？

射影行列

別の例として、射影行列の像や核を考えてみましょう。射影行列とは、\(P^2 =P\)を満たす正方行列のことです。

\(P\)の像と核については、

\[ \begin{aligned}\mathbb{R}^N = P(\mathbb{R}^N) \dot{+} \ker P\end{aligned} \]

という直和分解が成り立ちます。

ここで、像と核が\(P\)不変な部分空間であることを確かめてみましょう。

まず、像\(P(\mathbb{R}^N)\)は\(P\)不変です。定義式において、\(P(\mathbb{R}^N)\subset P(\mathbb{R}^N)\)は等号として当然成り立つので。

核\(\ker P =\{x \mid Px =0\}\)について。\(P(\ker P) \subset \ker P\)を示します。\(y \in P(\ker P)\)とすると、\(y= Px , x \in \ker P\)と表わせます。核の定義より、\(Px =0\)です。\(P^2=P\)に注意すれば、\(Py= PPx =Px =0\)なので、\(y\in \ker P\)が言えました。

以上、不変部分空間とは何か、固有空間、射影行列を例に紹介してきました。

何かの行列・作用素について不変な集合・空間という考え方は、数学全般で見られます（例えば群の作用について不変な集合、正規部分群）。

単に「不変」と略記されることが多いですが、「何の集合が」「何の変換について」不変なのか意識すると、意味がわかりやすくなるかと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。