どうも、木村(@kimu3_slime)です。
行列に対してランク、行列式、固有値といった量が定まります。それと同様に、線形写像に対しても、その表現行列によってランク、行列式、固有値が定義できます。
それが定義できるには、表し方によってランク、行列式、固有値が変わらないことを確かめなければなりません。一般に、ひとつの線形写像の表現行列には、基底の選び方によっていくつかの表し方があるので、それによって値が変わってしまったら困りますね。今回は、実際にそれが起こらないことを紹介します。
線形変換のランク、行列式、固有値
まず、定義域と行き先が一致する線形写像、線形変換\(f: V \to V\)について考えましょう。\(V\)は\(n\)次元の線形空間とします。
結論から言えば、異なる基底に関する表現行列を考えても相似になります。それを示しましょう。
\(f\)の基底\(E_A\)に関する表現行列を\(A_f\)、基底\(E_B\)に関する表現行列を\(B_f\)としましょう。
基底を対応させる線形写像(同型写像)は唯一つに決まるので、\(E_A\)に対応させるものを\(F:\mathbb{R}^N \to V\)、\(E_B\)に対応させるものを\(G:\mathbb{R}^N \to V\)とします。
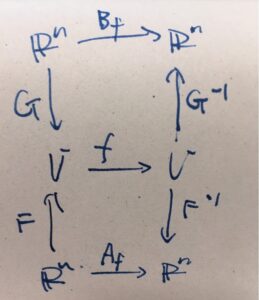
図に描けば関係性は上のようになっており、表現行列の定義から、\(A_f = F^{-1}\circ f \circ F\)、\(B_f = G^{-1}\circ f \circ G\)です。
この関係を整理するために、基底\(E_A\)から基底\(E_B\)への取り換えの行列を\(P\)としましょう。
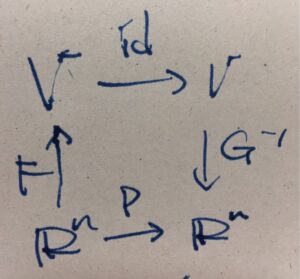
それは、恒等変換\(\mathrm{id}:V \to V\)の表現行列のことです。したがって、\(P = G^{-1} \circ \mathrm{id} \circ F=G^{-1} \circ F\)です。
以上によって、表現行列同士の関係をまとめましょう。\(f\)について整理すると、\(F \circ A_f \circ F^{-1} =f\)、\(G \circ B_f \circ G^{-1} =f\)となります。左辺が等しいことから、\(B_f =G^{-1}\circ F \circ A_f \circ F^{-1} \circ G\)です。ここで\(P=G^{-1} \circ F\)を使うと、\(B_f = P^{-1}A_f P\)が得られました。
これは行列\(A_f,B_f\)が相似であることの定義を満たします。したがって、相似な行列の一般論から、それらのランク、行列式、固有値、固有多項式、トレースが等しいことがわかりました。それらの量は、表現行列の表し方によらずに定まっています。
線形写像のランク
表現行列が正方行列とならないケース、一般の線形変換\(f:V \to W\)についても、ほぼ同様に議論できます。
線形写像\(V\)の次元を\(n\)、\(W\)の次元を\(m\)としましょう。
\(V\)の基底として\(E_{A}(V),E_{B}(V)\)、\(W\)の基底として\(E_{A}(W),E_{B}(W)\)という2種類を考えます。基底を対応させる線形写像を順に、\(F,G,H,J\)とします。基底\(E_{A}(V),E_{A}(W)\)に関する\(f\)の表現行列を\(A_f\)、\(E_{B}(V),E_{B}(W)\)に関する表現行列を\(B_f\)とします。図に表せば次の通り。
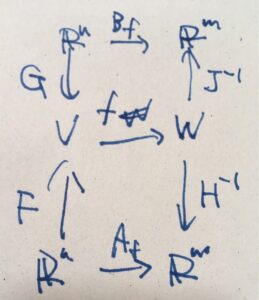
表現行列の定義から、\(A_f =H^{-1}\circ f \circ F\)、\(B_f =J^{-1}\circ f \circ G\)です。
また、\(E_{A}(V),E_{B}(V)\)の基底の取り換えの行列を\(P\)、\(E_{A}(W),E_B(W)\)に関しては\(Q\)とします。
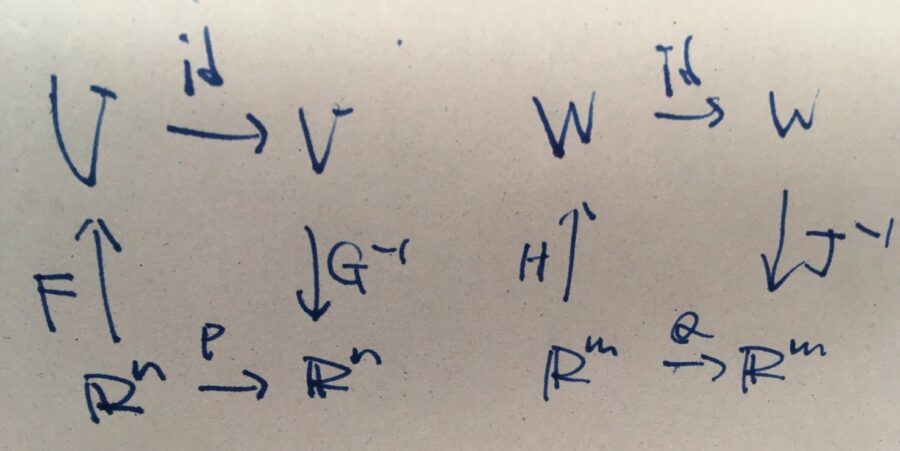
さきほどと同様の議論で、\(P=G^{-1}\circ F\)、\(Q= J^{-1}\circ H\)です。
\(f\)について整理すると、\(f=H\circ A_f \circ F^{-1}=J\circ B_f \circ G^{-1} \)となります。\(B_f\)について整理し、\(P,Q\)を使って表せば、
\[ \begin{aligned} B_f &= J^{-1}\circ H\circ A_f \circ F^{-1} \circ G \\&= Q A_f P^{-1} \end{aligned} \]
となりました。
この関係式が成り立つとき、ランクは等しい\(\mathrm{rank}A_f =\mathrm{rank}B_f\)です。
\(\mathrm{rank}B_f=r\)として、基本変形によって標準形になったとしましょう。
\[ \begin{aligned}R B_f S = \begin{pmatrix} I_r &O\\O&O \end{pmatrix}\end{aligned} \]
ランクの表現行列の関係式から、
\[ \begin{aligned}R Q A_f P^{-1} S = \begin{pmatrix} I_r &O\\O&O \end{pmatrix}\end{aligned} \]
です。\(P,Q\)は基底の取り換えであり、全単射、すなわち可逆行列です。したがって、線形独立なベクトルの本数=ランクを変えません。よって、\(A_f\)のランクも\(r\)であることがわかりました。
以上、線形写像のランク、行列式、固有値といった量は、表現行列の選び方によらずに定まっていることを紹介してきました。
この性質があるおかげで、例えば線形写像が単射・全射かどうかを、表現行列のランクによって判定することができます。
一般論としてはややこしいかもしれませんが、線形変換についてはシンプルにまとめられます。考える基底を変えても、表現行列は相似になるのです。基底を選ぶ自由さはあっても、ランク・行列式・固有値が変わらない程度には似た表現行列になるわけですね。
もちろん、今回の話を知らなくても、具体的に線形写像のランク・行列式・固有値を計算できます。ただ、そこで自由に基底を選んで恣意的な表現行列を考えて良い理由として、今回の話を思い出してもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版 (1982-07-09T00:00:01Z)
¥788 (中古品)
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社 (2015-12-22T00:00:01Z)
¥14,721 (コレクター商品)
東京大学出版会 (2019-03-08T00:00:00.000Z)
¥1,870
こちらもおすすめ
行列の相似とは:対角化との関係、不変量(ランク、行列式、固有値)