数列と関数は似ている：等差・等比数列と一次・指数関数

どうも、木村（@kimu3_slime）です。

高校数学では数列について学びますが、それは関数と似ている部分があります。

今回は、等差・等比数列と一次・指数関数の関係を紹介していきます。

等差数列と1次関数
等比数列と指数関数
こちらもおすすめ

等差数列と1次関数

等差数列とは、数列のある項とその次の項の差が一定であるような数列です。

例えば、\(a_n =3 n +1\)は等差数列です。隣り合う項を比較すると、\(a_{n+1}-a_n =(3n+3+1)-(3n+1)=3\)となるので。この\(n\)に依存しない差\(d= a_{n+1}- a_{n}\)を公差、\(a_1 =4\)を初項というのでした。

等差数列は、1次関数とよく似ています。

\(a_n = 3n+1\)に対応する1次関数は、\(f(x)= 3x+1\)です。

違いと言えば、数列では変数\(n\)が飛び飛びの数：自然数であるのに対し、関数では\(x\)を連続的な数：実数として考えることにあります。グラフも数列は飛び飛びで、関数ではつながった曲線になります。

数列は普通\(a_n\)といったように下付きの文字で変数を表しますが、それは関数のように\(f(x)\)と表すならば、\(a(n)\)という関数として見ることができます。数列は、自然数を定義域：変数とする一種の関数であると言えるわけですね。

等差数列は、一般的に次のように表されます。公差を\(d\)、初項を\(a_1\)として、

\[ \begin{aligned}a_n = d(n-1) +a_1\end{aligned} \]

と。これは1次関数として見れば、傾きが\(d\)で、\(n=1\)で\(a_1\)を通る直線です。すなわち、

\[ \begin{aligned}f(x) =d(x-1) +a_1\end{aligned} \]

に対応します。関数では\(x=0\)を中心に物事を考えますが、数列では\(n=1\)を初項として見ることが多いので、\(x-1\)の形が出てくる形になってずれているわけですね。

初めて等差数列と聞くと難しく感じるかもしれませんが、1次関数を考えているのと似たようなものです。

等比数列と指数関数

等比数列とは、数列の隣り合う項の比が一定であるような数列です。

例えば、\(a_n =5 \cdot 3^n\)は等比数列です。隣り合う項の比を取ると、\(\frac{a_{n+1}{a_n}}= \frac{5 \cdot 3^{n+1}}{5 \cdot 3^n}=3\)と一定になるので。この\(n\)に依存しない比\(r= \frac{a_{n+1}}{a_n}\)を公比というのでした。

等比数列は、指数関数とよく似ています。

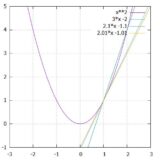
\(a_n =5 \cdot 3^n\)に似ているのは、\(f(x) = 5 \cdot 3^x\)です。

等比数列の一般項は、公比を\(a\)初項を\(a_1\)として、\(a_ n = a_1 r ^{n-1}\)と表されます。

これに対応する指数関数は、\(f(x) =a _1 r ^{x-1} \)です。指数関数で言えば、\(x\)が1増えるごとにかかる倍率\(r\)は、底と呼ばれるものですね。初項\(a_1\)は、べき乗の部分が\(r^{1-1}= r^0=1\)となるときの関数の値です。

以上、数列と関数の似ている点を紹介してきました。

数列と関数には、他にも類似点があります。