対数logの外し方、外せる条件と対数関数の性質

どうも、木村（@kimu3_slime）です。

数学の問題において、対数を外したいけれども、どうやって外せば良いか、外して良いのかどうか迷うことがあるかと思います。

今回は、対数の外し方に関する疑問を解消するための知識を解説します。

対数が外せる条件
変数分離法の例
対数不等式の注意点
こちらもおすすめ

対数が外せる条件

\(x>0,y>0\)とする。\(\log _a x = \log _a y\)ならば、\(x =y\)が成り立つ。

これが対数を外すための基本的な条件ですね。対数の底\(a\)が左辺と両辺で一致していて、両辺が\(\log\)ひとつの式である必要があります。

「両辺を\(\log\)で約分した」わけではないので、注意しましょう。（底が同じ）対数の値が等しいとき、中身（真数部分）も必ず等しくなる、という対数関数の性質です。

なぜこの性質は正しいのでしょうか？　それは\(f(x )= \log _a x\)のグラフを考えるとわかります。

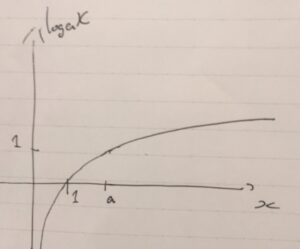
底が\(a>1\)のとき、\(f(x)=\log _a x\)は、真数\(x\)が大きくなると必ず大きな値を取ります。つまり、\(x<y\)ならば\(f(x) =\log_a x < \log_a y =f(y)\)が成り立つ。こういう関数を、（狭義）単調増加な関数と呼びます。

なぜ単調増加になるかといえば、その微分が\((\log _a x)^{\prime} =\frac{1}{(\log_e a)x}\)となり、\(a>1\)のときそれが常に正となるからです。一般に、関数の導関数が常に正ならば、単調増加な関数となります。

単調増加な関数ならば、\(\log\)を外す性質が導けます。「\(\log _a x = \log _a y\)ならば、\(x =y\)が成り立つ。」は、その対偶「\(x\neq y\)ならば\(\log _a x \neq \log _a y\)」に論理的に等しいです。

\(x\neq y\)と仮定します。まず\(x<y\)のケースを考えましょう。すると、対数の単調増加性から、\(\log_a x < \log_a y\)が導けます。特に、\(\log_a x \neq \log_a y\)です。\(x>y\)のときも同様です。よって、結論「\(\log _a x = \log _a y\)ならば、\(x =y\)が成り立つ。」が正しいとわかりました。

底が\(a<1\)のときは、\(x\)が大きくなると必ず\(f(x)\)は小さくなる、（狭義）単調減少な関数となります。

このときも同様の議論により、「\(\log _a x = \log _a y\)ならば、\(x =y\)が成り立つ。」が言えます。

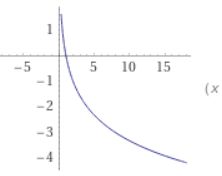
画像引用：log_{1/2} (x) – WolframAlpha

「\(\log _a x = \log _a y\)ならば、\(x =y\)が成り立つ。」という性質は、一般に関数の単射性と呼ばれる性質です。

「すべての\(x,y\)について、\(f(x) =f(y)\)ならば\(x=y\)」が成り立つ関数\(f\)は、単射であると定義されます。

\(f(x)= \log _a x\)という対数関数は、単射な関数です。単射な関数が両辺で等しい\(f(x)=f(y)\)という関係が得られたら、その関数を「外す」\(x=y\)ことができるわけです。

すべての関数が単射であるわけではありません。例えば、\(g(x)=x^2\)は単射ではありません。\(g(-1)=1 =g(1)\)ですが、だからといって\(-1 =1\)とは結論できませんね（間違い）。

一般には、（狭義）単調増加、または単調減少な実数値関数は、単射になります。例えば、\(h(x) =e^x\)といった指数関数は（狭義）単調増加です。\(e^x=e^y\)から、\(x=y\)を結論できます。\(e\)を「外せる」わけですね。

変数分離法の例

対数関数を外したい状況の例として、常微分方程式の変数分離法による解き方を例としましょう。微分方程式の話は、知らなくても大丈夫です。

例えば\(x\)を変数とする関数\(y(x)\)に関する微分方程式

\[ \begin{aligned}\frac{dy}{dx} = xy \end{aligned} \]

を解きたいとしましょう。両辺を\(y\)で割ることにより、\(x,y\)で分離させることができて、両辺を\(x\)について積分すれば

\[ \begin{aligned}\int \frac{1}{y} dy = \int x dx\end{aligned} \]

が得られます。この不定積分を計算すると、

\[ \begin{aligned}\log |y| = \frac{1}{2}x^2 +C\end{aligned} \]

です。ここで\(\log \)は自然対数\(\log _e\)のことです。

（\(\int \frac{1}{y} dy = \log |y|+C\)と絶対値がつくことに注意しましょう。この不定積分のもととなる\(\frac{d}{dy}\log |y| = \frac{1}{y}\)という式は、\(y>0,y<0\)のいずれでも成り立っています。\(\frac{1}{y}\)という\(y<0,y>0\)で定義された関数の原始関数を考えるには、\(\log y\)を考えると\(y<0\)で定義されておらず適切でないわけですね。）

\(\log |y| = \frac{1}{2}x^2 +C\)から\(y\)に関する式を得たいわけですが、そこで\(\log\)を外したいです。対数の外し方を思い出しましょう。

\(\log _a x = \log _a y\)ならば、\(x =y\)が成り立つ。

これを適用するために、右辺を\(\log\)の形に変形させます。\(\log _e e=1\)という基本的な性質から出発しましょう。両辺に同じ値をかけて \((\frac{1}{2}x^2 +C) \log _e e=\frac{1}{2}x^2 +C\)です。対数の指数に関する性質\(r \log_a b = \log_a b^r\)を用いれば、左辺は\(\log _e e^{(\frac{1}{2}x^2 +C)}\)となりました。

対数の基本的な性質について参考：逆の計算は定義に戻れ：負の数、分数、ルート、対数

もともとの式は、\(\log |y| = \log e^{(\frac{1}{2}x^2 +C)}\)となります。ここで対数を外せる性質（単射性）を用いれば、\(|y| =e^{(\frac{1}{2}x^2 +C)}\)と外せました。

よって、絶対値を外すと正負2通りの可能性があり、\(y(x) =\pm e^{(\frac{1}{2}x^2 +C)}\)が得られました。定数をわかりやすく捉えるならば、\( \pm e^{(\frac{1}{2}x^2 +C)}= \pm e^{\frac{1}{2}x^2 } e^{C} = A e^{\frac{1}{2}x^2 }\)と何らかの文字\(A\)で表せば良いでしょう。

対数不等式の注意点

対数を含む不等式も、基本的にはさきほどまでと同じような論理で対数を外すことができます。しかし注意すべき点があって、それは対数の底\(a\)が1より大きいか小さいかです。

例えば、\(\log _e x < \log_e 8\)から、\(x<8\)を結論するのは正しいです。しかし、\(\log_{\frac{1}{2} }x < \log _{\frac{1}{2}} 8\)から、\(x<8\)を導くのは間違いです。

実際、\(8= 2^3 =(\frac{1}{2})^{-3}\)なので、右辺は\(-3\)です。一方、\(x<8\)を満たす\(x\)、例えば\(x=\frac{1}{2}\)のとき左辺は\(1\)で、\(1<-3\)は成り立ちません。正しい結論としては、\(x>8\)と考えるべきだったのです。

最初に確認しましたが、\(f(x)= \log_a x\)は、\(a>1\)のとき単調増加、\(a<1\)のとき単調減少です。対数関数がいつでも増加していくようなイメージを抱くのは間違いなので注意しましょう。\(a<1\)のとき、\(\log_a x < \log _a y\)からは、逆向きの不等式\(x>y\)が得られます。

以上、対数logの外し方、外せる条件を紹介してきました。

外し方としては、両辺を同じ底の対数ひとつにまとめること\(\log_a x =\log_a y\)、その形になるように変形していくことです。はずせる理由は、対数関数の単調性、単射性にあります。

教科書や参考書では、こうした対数の計算は当たり前としてすっ飛ばされているかもしれませんが、この記事の話で納得してもらえたら嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。