グラフ理論における経路、連結性とは？

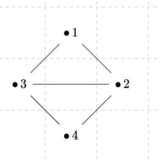
どうも、木村（@kimu3_slime）です。

今回は、グラフ理論における経路、連結性について紹介します。

経路とは
連結性と連結成分
こちらもおすすめ

経路とは

次の2つのグラフを見てください。

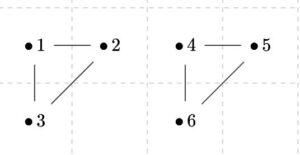
これら2つは、頂点の数、辺の数、次数列が一致するものの、グラフとして同型でないことが知られています。

感覚的に言えば、一方は2つの部分に分かれていて、もう一方は1つにまとまっているように見えます。この違いを説明するために、経路という考え方が役立ちます。

経路とは、おおざっぱにいえば、グラフの異なる頂点を辺で結んでいったものです。

例えば、\(1,2,3\)と進む経路は、\(1\)から出発して辺\(\{1,2\}\)を渡り\(2\)に着いて、続いて\(\{2,3\}\)を渡って……と考えられます。すなわち、\((1,\{1,2\},2,\{2,3\},3)\)と、頂点と辺が交互に並んだ列として表せます。

一般に、\(G=(V,E)\)をグラフ、\(v_0,\dots,v_T \in V\)、\(e_i=\{v_{i-1},v_{i}\}\in E\)とします。頂点と辺が交互に並んだ有限列\(P=(v_0,e_1,v_1,\dots,e_T,v_T)\)を、始点\(v_0\)から終点\(v_T\)までの経路、パス（path）と呼びます。ここで始点と終点以外の頂点\(v_1,\dots,v_{T-1}\)を内部頂点（internal vertices）と呼び、内部頂点がすべて異なる経路を単純経路（simple path）と呼びます。また、経路に含まれる辺の個数\(T\)を経路の長さ（length）と呼びます。

上のグラフにおいて、\((1,\{1,2\},2,\{2,3\},3,\{3,1\},1)\)という始点と終点が同じ経路が考えられます。一般に、始点と終点が一致する経路を、閉経路（closed path）と呼びます。さらに、長さ\(3\)以上の単純な閉経路はサイクル（cycle）と呼ばれるものです。

\((1,\{1,2\},2,\{2,1\},1)\)は閉経路ですが、サイクルではありません。行きと帰りの辺が一致していて、サイクルとは呼び難いですね。

経路の考え方は、平面や空間における曲線とよく似ています。両者には端点があり、その間がどうつながっているか指定したものです。自己交差を持たない曲線は単純曲線、端点が一致する曲線は閉曲線と呼ばれますが、これは単純経路、閉経路と対応したものです。

参考：曲線（1変数ベクトル値関数）とその微分について、

グラフ理論の用語は、文献によって意味合いが若干違うことがあるので注意しましょう。

例えば、単に経路と呼ぶとき、単純経路を仮定することがあります。そして、重複、往復を許した経路を歩道、ウォーク（walk）として区別することがあります。この記事では、経路を一般的な語（単純性を必ずしも仮定しない）として使います。また、例えば path が道と呼ばれることもあります。

文脈に応じて、重複が許されているのか許されていないかを読み取るのが大事です。

連結性と連結成分

いよいよ、連結性を定義しましょう。

グラフ\(G=(V,E)\)が連結である（connected）とは、任意の頂点\(x,y \in V\)に対し、\(x\)から\(y\)への単純な経路が存在することです。連結でないことは、非連結である（disconnected）とも呼ばれます。

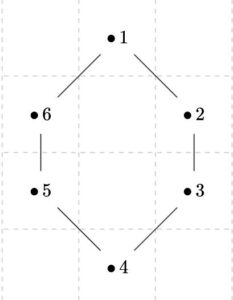
上側のグラフは連結でなく、下側のグラフは連結です。

上のグラフが連結でないことを示すには、ある\(2\)つの頂点をつなぐ経路が存在しないことを示せば良いです。\(1,4\)をつなぐ経路は存在しません。任意に\(v\in\{1,2,3\}\)、\(w \in \{4,5,6\}\)とすると、\(\{v,w\} \not \in E(G)\)です。\(1,4\)をつなぐ単純な経路が存在したと仮定すると、ある\(v\in\{1,2,3\}\)、\(w \in \{4,5,6\}\)で\(\{v,w\} \in E(G)\)が成立することになり、矛盾します。

参考：「すべての」「存在する」「一意性」とは？証明の書き方

この2つのグラフは、グラフとして同型でないことが示せます。

一般論として、グラフ\(G_1,G_2\)が同型であるとき、\(G_1\)が連結であることと\(G_2\)が連結であることは同値となります。その対偶が、連結なグラフと非連結なグラフは、同型でないということです。

グラフの同型写像を\(F:G_1 \to G_2\)とし、\(G_1\)が連結であると仮定しましょう。任意に\(v,w \in V(G_2)\)を選びます。\(G_1\)の連結性より、\(F^{-1}(v),F^{-1}(w)\)を結ぶ単純な経路が存在します。\(P=(F^{-1}(v),e_1,\dots,e_T,F^{-1}(w))\)と表しましょう。\(F(P)=(v,F(e_1),\dots,F(e_T),w)\)と置くと、\(F(P)\)は\(v,w\)を結ぶ\(G_2\)の経路です。\(e_i=\{v_{i-1},v_{i}\}\in E(G_1)\)ですが、\(F\)がグラフの同型写像であることにより、\(F(e_i)=\{F(v_{i-1}),F(v_{i})\}\in E(G_2)\)なので。さらに、\(P\)は単純な経路で、\(F\)は単射なので、\(F(P)\)は単純な経路です。よって、\(G_2\)が連結であることが示せました。

一般論として、経路、単純経路の同型写像による像、逆像は、また経路、単純経路となります。

グラフには、その内部でつながっている部分を考えることができます。

グラフの頂点\(x,y \in V\)に対して、\(x\sim y\)という関係\(\sim\)を、\(x,y\)を結ぶ経路が存在する、という条件で定めましょう。

この関係は、同値関係となります。長さ\(0\)の経路を考えれば、\(x\sim x\)です。\(x\sim y\)のとき、経路を逆にして考えれば、\(y \sim x\)です。\(x \sim y, y\sim z\)のとき、それをつなげた経路を考えられるので、\(x\sim z\)が成り立ちます。

\(v\)の経路があるという関係\(\sim\)による同値類\(C(v):=\{ w \in V \mid v \sim w \} \)を、\(v\)の連結成分（connected component）と呼びます。頂点の集合は、（互いに共通部分を持たない）いくつかの連結成分に必ず分かれます。

例えば、上のグラフでは、\(C(1)=C(2)=C(3)=\{1,2,3\}\)と\(C(4)=C(5)=C(6)=\{4,5,6\}\)という2つの連結成分に分かれます。2つ以上の連結成分を持つグラフは、非連結です。

このグラフでは、連結成分は1つ\(C(1)=\cdots =C(6)=V\)しかありません。連結成分が1つであるグラフは、連結です。

一般に、連結成分の同型写像による像も、連結成分になります。

以上、グラフ理論における経路、連結性について例を交えて紹介してきました。

今回はグラフの連結性を考えましたが、より一般的な位相空間論でも、弧状連結性や連結性という概念を考えます。そちらも学んでみると良いでしょう。

グラフの次数と合わせて、連結性はグラフの特徴を表す概念なので、グラフの具体例を作ったら連結かどうか、考えてみましょう。

木村すらいむ（@kimu3_slime）でした。ではでは。