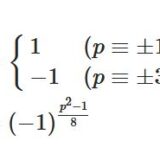ルジャンドル記号の性質、平方剰余の第一補充法則を解説

どうも、木村（@kimu3_slime）です。

今回は、ルジャンドル記号の性質と、ガウスの補題を解説します。

ルジャンドル記号とその性質
第一補充法則
こちらもおすすめ

ルジャンドル記号とその性質

\(n\)を正の整数とします。整数\(a\)が、ある平方数\(x^2\)により\(x^2 \equiv a \,(\mathrm{mod} \,n)\)と表せるとき、\(a\)は\(n\)を法とする平方剰余と呼ぶのでした。\(n\)が奇素数\(p\)であり、\(a,p\)が互いに素であるとき、次の記号を使って平方剰余を言い換えましょう。

\[ \begin{aligned}\left(\frac{a}{p}\right)= \begin{cases}1 & (aがpを法とする平方剰余のとき )\\-1 & (aがpを法とする平方非剰余のとき)\end{cases}\end{aligned} \]

この記号\(\left(\frac{a}{p}\right)\)をルジャンドル記号（Legendre symbol）と呼びます。

平方剰余かどうかを調べるには、ルジャンドル記号の値を計算すれば良いということになります。今回は、その性質を調べていきましょう。

\(p\)を奇素数、\(a,b\)を\(p\)と互いに素な整数とする。次の性質が成り立つ。

\(a \equiv b \,(\mathrm{mod} \,p)\)ならば、\(\left(\frac{a}{p}\right)=\left(\frac{b}{p}\right)\)
\(\left(\frac{a^2}{p}\right)=1\)
\(\left(\frac{a}{p}\right) \equiv a^{\frac{p-1}{2}}\,(\mathrm{mod} \,p)\)
\(\left(\frac{ab}{p}\right)=\left(\frac{a}{p}\right)\left(\frac{b}{p}\right)\)
\(\left(\frac{1}{p}\right)=1\)、\(\left(\frac{-1}{p}\right)=(-1)^{\frac{p-1}{2}}\)

一般的な証明に入る前に、まずはこうした性質が実際に成り立っているのか、簡単な具体例で考えてみます。

\(p=5\)のとき、ルジャンドル記号を計算してみます。すなわち、平方数で表されるか判定すれば良いです。まず、\(1^2 \equiv 1\)、\(2^2 \equiv 4\)、\(3^2 \equiv 4\)、\(4^2 \equiv 1\)です。\(5\)以上の数については、例えば\(6\equiv 1\)なので、この計算ですべての場合が尽くされています。\(1,4\)は平方数として表されています。\(2,3\)は平方数として表されえません。したがって、\(\left(\frac{1}{5}\right)=\left(\frac{4}{5}\right)=\left(\frac{6}{5}\right)=1\)、\(\left(\frac{2}{5}\right)=\left(\frac{3}{5}\right)=-1\)です。

1.について。\(1\equiv 6\)のとき、\(\left(\frac{1}{5}\right)=\left(\frac{6}{5}\right)\)は成り立っています。これはほぼ当然です。

2.について。\(a^2\)について考えると、例えば\(4,9\equiv 4,16\equiv 1\)が登場しますが、どれも平方剰余です。\(\left(\frac{2^2}{5}\right)=\left(\frac{3^2}{5}\right)=\left(\frac{4^2}{5}\right)=1\)は成り立ちます。

3.について。\(a^{\frac{p-1}{2}}=a^2\)で、\(1^2 \equiv 4^2 \equiv 1\)、\(2^2 \equiv 3^2\equiv -1\)が成り立つので、成り立ちます。

4.について。\(a=2,b=3\)とすると、\(\left(\frac{6}{5}\right)=1\)、\(\left(\frac{2}{5}\right)\left(\frac{3}{5}\right)=(-1)^2=1\)で成り立ちます。\(a=3,b=4\)とすると、\(\left(\frac{12}{5}\right)=\left(\frac{2}{5}\right) =-1\)、\(\left(\frac{3}{5}\right)\left(\frac{4}{5}\right)=1\cdot(-1)\)で成り立ちます。

5.について。\(\left(\frac{1}{p}\right)=1\)は、\(1\)が平方剰余なので良いでしょう。\(\left(\frac{-1}{p}\right)=\left(\frac{4}{p}\right)=1\)、\((-1)^{\frac{p-1}{2}}=1\)で成り立っています。

では、一般に示しましょう。

1.について。\(x^2 \equiv a\,(\mathrm{mod} \,p)\)、\(x^2 \equiv b\,(\mathrm{mod} \,p)\)は、仮定より\(a \equiv b\,(\mathrm{mod} \,p)\)のとき、同じ解を持ちます。したがって、\(a\)が平方剰余であることと\(b\)が平方剰余であることは同値になり、\(\left(\frac{a}{p}\right)=\left(\frac{b}{p}\right)\)です。

2.について。\(a^2\)は平方数であり、したがって常に平方剰余です。\(x\equiv a^2\)を満たす解は\(x=a\)として存在するので。よって、\(\left(\frac{a^2}{p}\right)=1\)です。

3.について。これはオイラーの判定条件（平方剰余であることは\(a^{\frac{p-1}{2}} \equiv 1\,(\mathrm{mod} \,p)\)と同値）によるものです。そもそも、ルジャンドル記号はオイラーの判定条件に合うように導入されたと言えるでしょう。

4.について。3.を使って示せます。まず、\(\left(\frac{ab}{p}\right)\equiv (ab)^{\frac{p-1}{2}} \\ \equiv a^{\frac{p-1}{2}}b^{\frac{p-1}{2}} \equiv \left(\frac{a}{p}\right)\left(\frac{b}{p}\right) \)が成り立ちます。左辺の値は\(\pm 1\)、右辺も\(\pm 1\)しかなく、\(p\)が奇素数なので\(1 \not \equiv -1\)です。したがって、\(\left(\frac{ab}{p}\right)=\left(\frac{a}{p}\right)\left(\frac{b}{p}\right)\)が示せました。

5.について。\(1^2 \equiv 1\)なので、\(1\)は平方剰余であり、\(\left(\frac{1}{p}\right)=1\)です。3.において\(a=-1\)とすれば、\(\left(\frac{-1}{p}\right) \equiv (-1)^{\frac{p-1}{2}}\,(\mathrm{mod} \,p)\)です。左辺の値は\(\pm 1\)、右辺も\(\pm 1\)しかないので、\(\left(\frac{-1}{p}\right) = (-1)^{\frac{p-1}{2}}\)が得られました。

第一補充法則

さきほど示した性質は、さらに次のように言い換えることができます。

\(p\)を奇素数とする。次の等式が成り立つ。

\[ \begin{aligned}\left(\frac{-1}{p}\right)= \begin{cases}1 & (p\equiv 1\,(\mathrm{mod} \,4))\\-1 & (p\equiv 3 \,(\mathrm{mod} \,4))\end{cases}\end{aligned} \]

これは平方剰余の第一補充法則（first supplement to quadratic reciprocity）と呼ばれています。（後に紹介する）平方剰余の法則を補うような、基本的な法則というわけです。

なぜこれが導けるか。一般に、\(\left(\frac{-1}{p}\right)=(-1)^{\frac{p-1}{2}}\)です。その値が\(1\)となるのは、\(\frac{p-1}{2}\)が偶数、すなわち\(p-1\)が\(4\)の倍数、\(p\equiv 1\,(\mathrm{mod} \,4)\)のときです。その値が\(-1\)となるのは、\(\frac{p-1}{2}\)が奇数、\(p-1\)が\(4\)で割ってあまり\(2\)、\(p\equiv 3 \,(\mathrm{mod} \,4)\)のときです。

これまでの性質を用いて、ルジャンドル記号を計算し、平方剰余かどうかを判定してみましょう。

\(p=43\)について考えます。\(a=27\)としましょう。ここで、\(3^2=9\)で割ると単純になります、\(\left(\frac{27}{43}\right) =\left(\frac{3}{43}\right)\left(\frac{3^2}{43}\right)=\left(\frac{3}{43}\right)\)です。オイラーの判定条件を用いれば、\(\left(\frac{3}{43}\right)\equiv 3^{21}\)です。\(3^4 \equiv 81 \equiv -5\)なので、\(3^{20}\equiv (-5)^5\)。\(5^3 \equiv -4\)なので、\((-5)^5 \equiv 4\cdot 5^2 \equiv 14\)。よって、\(3^{21} \equiv 3\cdot 3^{20} \equiv 3\cdot 14 \equiv -1\)。\(27\)は\(43\)を法とした平方非剰余であることがわかりました。

第一補充法則からは、\(x^2 \equiv -1 \,(\mathrm{mod} \,p)\)が解を持つかどうかすぐに判定できます。\(p\)を\(4\)で割ってあまり\(1\)ならば解を持ち、\(4\)で割ってあまり\(3\)ならば解を持たないわけです。例えば、\(p=5,13,17,29\)のときは解を持ち、\(p=7,11,19,23\)のときは解を持たないことがわかります。

以上、ルジャンドル記号の性質、平方剰余の第一補充法則を紹介しました。

第一充足法則からは、\(4k+1\)の形をした素数が無限に存在することや、フェルマーの二平方定理（\(p\)が2つの平方数の和で表せることと、\(p\equiv 1\,(\mathrm{mod} \,4)\)は同値）を示せることも知られています。応用が幅広いですね。

「平方数として表されるか？」という問題は、ルジャンドル記号の計算に落とし込むと、かなり簡単になります。ぜひ実際に試してみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。