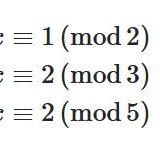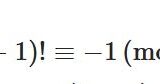フェルマーの小定理、フェルマーテスト、擬素数とは何か

どうも、木村（@kimu3_slime）です。

今回は、整数論におけるフェルマーの小定理、フェルマーテスト、擬素数とは何かについて紹介します。

フェルマーの小定理とは
フェルマーテスト、擬素数とは
こちらもおすすめ

フェルマーの小定理とは

フェルマーの小定理（Fermat’s little theorem）は、次の内容です。

\(a\)を整数とする。\(p\)を素数で、\(a\)を割り切らない\(p \not \mid a\)（\(a,p\)は互いに素）とする。このとき、次の整数の合同が成り立つ。

\[ \begin{aligned}a^{p-1} \equiv 1 \,(\mathrm{mod}\, p)\end{aligned} \]

結論は、\(a^{p-1}-1 \)は常に\(p\)で割り切れる、と言い換えても同じですね。この主張は、1995年に解決された有名なフェルマー予想、フェルマーの最終定理と区別するために、小定理と呼ばれています。

小定理がどんな主張をしているのか、まずは具体例で確かめてみましょう。

\(p=2\)のとき、仮定より\(a\)は奇数でなければなりません。\(a^{p-1}=a\)なので、奇数のあまりは\(1\)、という内容です。普通ですね。

\(p=3\)のとき、\(a^{p-1}=a^2\)であり、平方数の\(3\)で割ったあまりを考えることになります。一般には、平方数を\(3\)で割ったあまりは0または1で、2のケースが否定されるのでした。小定理の仮定は、\(p=3\)の倍数でない整数\(a\)について考えているので、\(a\)を3で割ったあまりが0でないケース、したがって\(a^2 \)を3で割ったあまりが0でないケースを考えていることになります。つまり、残されたケース\(a^2 \equiv 1 \,(\mathrm{mod}\, 3)\)しかありえないわけで、確かに小定理は正しいです。

\(p=5\)のときはどうでしょうか。整数\(a\)を\(p\)で割ったあまりを\(r\)とすると、\(a \equiv r \,(\mathrm{mod}\, 5)\)で、\(0\leq r \leq 4\)です。仮定より\(a\)が\(5\)の倍数である可能性は否定されているので、\(1\leq r \leq 4\)となります。

ここで、\(a \not \equiv 2a \,(\mathrm{mod}\, 5)\)がわかります。仮に\(a \equiv 2a \,(\mathrm{mod}\, 5)\)とすると、\(a,5\)が互いに素なので、合同式の性質より\(1 \equiv 2 \,(\mathrm{mod}\, 5)\)が導かれてしまい、矛盾するので。同様の議論で、\(a,2a,3a,4a\)は\(5\)を法として互いに合同でないことがわかります。

つまり、それぞれが\(1,2,3,4\)のいずれかに\(5\)を法として互いに合同です。したがって、これらの積を取っても合同式は成り立つので、\(a\cdot 2a\cdot 3a\cdot 4a \equiv 1\cdot 2\cdot 3\cdot 4 \,(\mathrm{mod}\, 5)\)です。整理すると、\(a^{p-1} (p-1)! \equiv (p-1)! \,(\mathrm{mod}\, 5)\)ですね。\(p\)と\((p-1)!\)は互いに素なので、合同式を割った式も正しく、\(a^{p-1} \equiv 1 \,(\mathrm{mod}\, 5)\)が導かれました。

この議論は一般化できて、それが証明となります。省略気味に述べましょう。

\(a,p\)は互いに素なので、\(a\)を\(p\)で割ったあまり\(r\)は、\(r=1,2,\cdots,p-1\)のいずれかです（\(0\)が否定される）。

そして、\(a,2a,\cdots ,(p-1)a\)は、\(p\)を法として互いに合同ではありません。仮に合同になってしまうとすると、\(a,p\)が互いに素であることから、偽の合同式が導かれるので。

したがって、\(a,2a,\cdots ,(p-1)a\)は、\(r=1,2,\cdots,p-1\)のいずれかに合同です。その積を取っても合同式は成り立つので、\(a^{p-1} (p-1)! \equiv (p-1)! \,(\mathrm{mod}\, p)\)が成り立ちます。\(p\)と\((p-1)!\)は互いに素なので、合同式を割った式も正しく、\(a^{p-1} \equiv 1 \,(\mathrm{mod}\, p)\)が導かれました。

フェルマーの小定理は、オイラーによって\(p\)が素数でないケースまで一般化されたものが知られています。

\(a\)を整数とする。\(n\)を正の整数で、\(a\)を割り切らない\(n \not \mid a\)（\(a,n\)は互いに素）とする。このとき、次の整数の合同が成り立つ。

\[ \begin{aligned}a^{\phi(n)} \equiv 1 \,(\mathrm{mod}\, n)\end{aligned} \]

ここで、\(\phi (n)\)は\(1\)から\(n\)までの整数のうち、\(n\)と互いに素な整数の個数を表す（オイラーの\(\phi\)関数）。

\(n\)が素数\(p\)のとき、\(p\)と\(1,2,\cdots,p-1,p\)で互いに素なのは\(1,2,\cdots,p-1\)の\(p-1\)個なので、\(\phi(p)=p-1\)です。フェルマーの小定理は、この定理の特殊なケースだった、と見れるわけですね。

オイラーの\(\phi\)関数、オイラーによる一般化された定理は、別の記事で紹介予定。

フェルマーテスト、擬素数とは

フェルマーの小定理は、\(p\)が素数のときにある条件を必ず満たす、という主張です。その対偶を取れば、素数でないことの十分条件が得られます。

\(a\)は整数、\(n\)は正の整数で、\(a,n\)は互いに素とする。

\[ \begin{aligned}a^{n-1} \not \equiv 1 \,(\mathrm{mod}\, n)\end{aligned} \]

を満たすならば、\(n\)は素数ではない（合成数である）。

フェルマーテストは、これを用いた\(n\)が素数かどうかの（確率的な）判定法です。

まず\(n\)を決め、ある\(a\)について、\(a^{n-1} \not \equiv 1 \,(\mathrm{mod}\, n)\)かどうかを確かめます。\(a^{n-1} \not \equiv 1 \,(\mathrm{mod}\, n)\)ならば、フェルマーの小定理の対偶より、必ず\(n\)は素数ではありません。

逆に、\(a^{n-1} \equiv 1 \,(\mathrm{mod}\, n)\)が成り立つならば、\(n\)が素数である可能性があります。このとき、\(n\)は\(a\)を底とした確率的素数、おそらく素数（probably prime）と呼びましょう。

いくつもの\(a\)について確率的素数であるならば、\(n\)は本当に素数である確率は高くなるでしょう。この確率的な素数判定法は、フェルマーテスト（Fermat primality test）と呼ばれています。

いくつかの\(a\)について確率的素数であるからといって、実際には素数でない可能性もあります。素数でない確率的素数を、擬素数（psudoprime）と呼びます。

例えば、\(n=7\)とすると、\(2^6=64 \equiv 1\,(\mathrm{mod}\, 7)\)で、\(3^6=729 \equiv 1\,(\mathrm{mod}\, 7)\)です。\(n\)は確率的素数です（実際、素数です）。\(n\)が素数のときは、\(a^{n-1} \equiv 1 \,(\mathrm{mod}\, n)\)しか成り立ちようがありません（フェルマーの小定理）。

\(n=91\)、\(a=3\)について調べてみましょう。\(3^6 =729 \equiv 1 \,(\mathrm{mod}\, 91) \)が基準として使いやすいですね。\(3^{90}=(3^6)^{15} \equiv 1^{15} \equiv 1 \,(\mathrm{mod}\, 91) \)です。つまり、\(91\)は\(3\)を底とした素数です。しかし、\(91=7\cdot 13\)で素数ではありません。よって、\(91\)は擬素数の例と言えました。

実は、フェルマーテストではどうやっても確率的素数になるが、実際には素数ではない数（擬素数）が存在します。\(n\)と互いに素なすべて整数\(a\)に対して、\(a^{n-1} \equiv 1 \,(\mathrm{mod}\, n)\)を満たす数\(n\)。それはカーマイケル数と呼ばれ、\(561,1105,\dots\)など無数にあることが知られています。

約数で割って素数かどうか判定する方法、試し割り法のような素数判定法は、確率的判定法に対して、決定的判定法と呼ばれます。必ず判定できるかわりに、どうしても計算に非現実的な時間がかかってしまいます。

それに対して、フェルマーテストのような確率的判定法は、確実ではないものの、計算が素早いです。フェルマーテストを改良した確率的判定法、ミラー-ラビン判定法やベイリー-PSW判定法が知られています。暗号の一種・RSA暗号では、大きな素数同士の積を考えますが、大きな素数を見つけるためには確率的判定法が役立つわけです。

以上、フェルマーの小定理、フェルマーテスト、擬素数とは何か紹介してきました。

\(a^{p-1} \equiv 1 \,(\mathrm{mod}\, p)\)は、非常にシンプルな形をしていますね。そして確率的素数判定や暗号にも応用されています。素数やその応用（暗号など）考えると、フェルマーの小定理は驚くべき結果と言えるのではないでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。