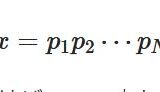どうも、木村(@kimu3_slime)です。
今回は、スカラー場やベクトル場の面積分とは何か、その計算例を紹介します。
スカラー場の面積分
ある曲面において、重さや熱量が場所によって違って分布しているような状況を考えましょう。その曲面における合計が、曲面の総重量、総熱量であり、それを求める計算が面積分です。
曲面\(S \subset \mathbb{R}^3\)が、\(p: \mathbb{R}^2 \to \mathbb{R}^3\)によってパラメータ表示されているとしましょう。スカラー場\(f: S \to \mathbb{R}\)の面積分(surface integral)は、
\[ \begin{aligned} \int _S f :=\int _U f(p(x,y)) \| p_x\times p_y \|dxdy\end{aligned} \]
と定義されます。
線積分の定義\(\int _c f :=\int_a ^b f(c(t)) \| c^{\prime }(t)\| dt\)を思い出すと、面積分の定義と似たものです。
特に\(f=1\)という定数関数のときは、面積分は\(U\)の曲面積に一致していますね。
\(S\)を半径\(r\)の球面とするとき、\(S\)上の点は\(p(\theta, \phi )=r(\sin \theta \cos \phi, \sin \theta \sin \phi, \cos \theta )\)と表せて、\(\|p_{\theta} \times p_{\phi}\| =r ^2 \sin \theta\)となります。
\(f(x,y,z)=x^2+y^2+z^2\)の\(S\)上の面積分を計算してみましょう。\(f(p(\theta, \phi )) =r^2\)なので、
\[ \begin{aligned} \int _S f &=\int _0 ^{2\pi } \int_0 ^{\pi} r^2 r^2 \sin \theta d\theta d \phi \\ &=2\pi r^4 [-\cos \theta] _0 ^{\pi} \\ &= 4\pi r^4\end{aligned} \]
となります。\(f\)を重さと見れば、\(r\)を変化させたとき、\(r^4\)に比例して増減するわけですね。
線積分で行ったのと同様に、曲面の重心は次のように定義されます。
\[ \begin{aligned}\bar{x} = \frac{\int _S x f}{\int _S f}\end{aligned} \]
今回の例\(f(x,y,z)=x^2+y^2+z^2\)では、
\[ \begin{aligned} \int _S xf &=\int _0 ^{2\pi } \int_0 ^{\pi} r\sin \theta \cos \phi r^2 r^2 \sin \theta d\theta d \phi \\ &=r^4 \int_0 ^{2\pi} \cos \phi d\phi \int _0 ^{\pi}(\sin \theta)^2 d\theta \\ &= 0\end{aligned} \]
なので、\(\bar{x}=0\)です。\(y,z\)方向の計算も同様に行えば、原点が重心となっていることがわかります。
ベクトル場の面積分
水の流れや、電気や磁気によって空間内の各点で受ける力を\(F\)と表すと、\(F\)はベクトル場(ベクトル値関数)\(F:\mathbb{R}^3 \to \mathbb{R}^3\)として捉えられます。
空間内のある曲面\(S\)を考えて、\(S\)を通り抜ける\(F\)はどのくらいの量あるのでしょうか。それを捉える手段が、ベクトル場の面積分です。
\(S\)の外向き単位法線ベクトルを\(n\)とし、それを基準にしましょう。\(n\)に直交する\(F\)はカウントせず、\(n\)と同じ向きを正、逆向きを負としてカウントするには、\(\langle F,n\rangle\)を考えれば良いです。
\[ \begin{aligned}\int _S \langle F,n\rangle\end{aligned} \]
をベクトル場\(F\)の\(S\)における面積分(integral of the vector field along the surface)と呼びます。
\(S\)が\(p(x,y)\)によってパラメータ表示されているとき、法線ベクトルは外積によって表せます。すなわち、\(n = \frac{ p_x\times p_y }{ \| p_x\times p_y \|}\)です。これと面積分の定義を組み合わせれば、
\[ \begin{aligned}\int _S \langle F,n\rangle= \int _U \langle F(p(x,y)),p_x\times p_y\rangle dx dy\end{aligned} \]
と計算できます。
これはベクトル場の線積分の定義\(\int _c f :=\int_a ^b \langle F(c(t)) ,c^{\prime }(t) \rangle dt\)とよく似ています。曲線に接するベクトルが\(c^{\prime }\)であり、曲面の法線ベクトルが\(p_x\times p_y\)です。
ベクトル場の面積分を計算してみましょう。
\(S\)を半径\(r\)の球面とすると、そのパラメータ表示\(p(\theta,\phi)\)の外積は\(p_{\theta} \times p_{\phi} =r \sin \theta \,p(\theta,\phi)\)となります。
\(F(x,y,z)=(-x/r^3,-y/r^3,-z/r^3)\),\(r=\sqrt{x^2+y^2+z^2}\)なるベクトル場を考えます。これは万有引力の法則、電荷に関するクーロンの法則を表すものです。
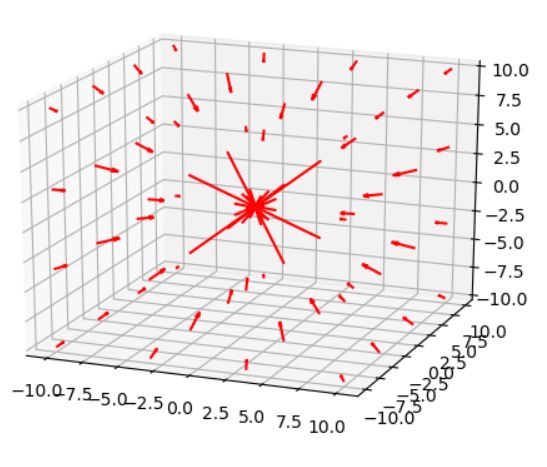
\(F=-\frac{1}{r^3}(x,y,z)=-\frac{1}{r^3}p(\theta,\phi)\)なので、\(\langle F,p_{\theta} \times p_{\phi} \rangle=-\frac{1}{r^2} \sin \theta \langle p(\theta,\phi),p(\theta,\phi)\rangle=-\sin \theta\)となります。よって、面積分は
\[ \begin{aligned} \int _S \langle F,n\rangle&= \int _0 ^{2\pi } \int_0 ^{\pi}\langle F(p(\theta,\phi)),p_\theta \times p_\phi \rangle d\theta d\phi \\ &=2\pi [\cos \theta]_0^\pi \\ &= -4 \pi \ \end{aligned} \]
となりました。
\(F\)を電場と考える時、その面積分は、電気力線の本数を(符号付きで)数えたことになります(つまり、電気力線とは面積分によって定義される量)。点電荷に関するガウスの法則によると、電気力線の本数を\(N\)として\(N=4\pi k |Q|\)が成り立ちます。今回は\(k=1,Q=-1\)のときに、クーロンの法則(逆2乗力)からこれを導いたわけです。
ガウスの法則は、\(\int_S \langle E ,dS\rangle=\frac{Q}{{\varepsilon}_0} \)といったように表されるものです。
以上、スカラー場とベクトル場の面積分、その計算例を紹介してきました。
密度や流体、電場や磁場を3次元空間で考えたときに、自然と登場してくる量なので、特殊な例から計算できるようになってみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740
こちらもおすすめ
ベクトル値関数をベクトル場として描いてみよう:ヤコビ行列と線形近似